Question
One cosmic ray neutron has a velocity of relative to the Earth. (a) What is the neutron’s total energy in MeV? (b) Find its momentum. (c) Is in this situation? Discuss in terms of the equation given in part (a) of the previous problem.
Final Answer
- No, only when
Solution video
OpenStax College Physics, Chapter 28, Problem 60 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
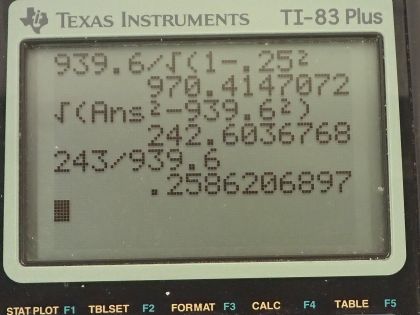
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A neutron has a velocity with respect to Earth of 0.250 times c and I also looked up in problem [58] that its rest mass energy is 939.6 megaelectron volts. Part (a) asks us for the total energy of this neutron and that's going to be γ times its rest mass energy so that's γ times E naught and γ is 1 over square root 1 minus v squared over c squared so when we substitute that in, we get this formula here so the total energy then is 939.6 megaelectron volts divided by square root of 1 minus 0.250c squared over c squared and that is 970 megaelectron volts. Part (b) asks us to find the momentum. So we have this relativistic expression for momentum in terms of energy and we can subtract the mc squared squared from both sides and that is momentum times speed of light squared equals the total energy squared minus the rest mass energy squared where I have substituted E naught in place of mc squared then take the square root of both sides and momentum times speed of light then is the square root of total energy squared minus rest mass energy squared and then divide both sides by c and you get this expression for momentum. So that's the square root of 970.41 megaelectron volts squared that we found in part (a) minus 939.6 megaelectron volts squared divided by c and this is 243 megaelectron volts per c. It's kind of a strange unit for momentum but it's equivalent to kilogram meters per second but it's just a more common unit to use in this context of tiny particles. Now in part (c), we are asked is the total energy approximately equal to momentum times speed of light? And in this case, it's not because the total energy is 970 megaelectron volts whereas momentum is 243 megaelectron volts per c so if we multiply it by c, the answer is 243 megaelectron volts and that's not the same... not even close! And we use this equation given to us in problem [59] and pc squared over mc squared squared equals γ squared minus 1, which is approximately γ squared when pc is much more than mc squared. Well, we can see in this case that pc divided by this denominator— where I have just taken them both to the power of 1 here just to illustrate how they compare— it's 243 divided by 939.6, which is 0.26 and this number shows that pc is much less or is less than E naught, which is mc squared and so it violates this condition here and so pc is not much much greater than the rest mass energy and so that formula doesn't quite work in this case; total energy is not approximately equal to momentum times speed of light because the speed is too slow here.