Question
If a galaxy moving away from the Earth has a speed of 1000 km/s and emits 656 nm light characteristic of hydrogen (the most common element in the universe). (a) What wavelength would we observe on the Earth? (b) What type of electromagnetic radiation is this? (c) Why is the speed of the Earth in its orbit negligible here?
Final Answer
- This is visible light.
- The orbital speed is only 3% of the recession speed of the galaxy. The orbital speed is insignificant.
Solution video
OpenStax College Physics, Chapter 28, Problem 24 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
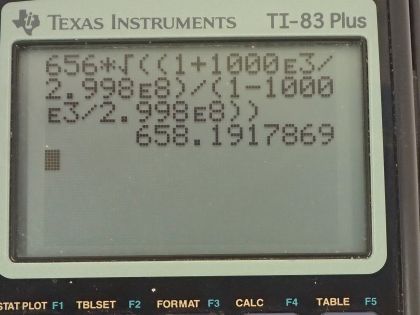
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A galaxy is moving away from the Earth with a speed of 1000 kilometers per second so that's 1000 times 10 to the 3 meters per second moving away means that this velocity, u, gets assigned a positive. The wavelength that the galaxy, which is the source is emitting, is 656 nanometers so somebody who's in the reference frame of the galaxy will report this as the emission frequency or sorry emission wavelength of the light. So the wavelength observed from the Earth then is going to be that source wavelength times square root of 1 plus u over c divided by 1 minus u over c. So that's 656 nanometers times the square root of 1 plus a 1000 times 10 to the 3 meters per second divided by speed of light divided by 1 minus 1000 times 10 to the 3 meters per second divided by speed of light this works out to 658 nanometers. We expected our answer to be a bigger number than the source and so doing that reality check is always useful to see if you have a sense of whether your answer is correct or not and sure enough 658 nanometers is greater than 656 nanometers. So galaxies receding from the Earth should give red-shifted wavelength, which is to say that the wavelengths are stretched. Okay! This is visible light and kind of an orangy-red probably. Part (c) says why do we ignore the speed of the Earth in its orbit? Well, let's figure out what that orbital speed is and it's going to be the circumference of its orbit, which is 2π times its average distance from the Sun so that's 2π times 149.6 times 10 to the 9 meters and we divide that by the time it takes to make a full circle, which is a year converted into seconds and that's 2.981 times 10 to the 4 meters per second. And then figure out what that speed is as a ratio of the speed of the galaxy receding so this works out to 0.0298. So the orbital velocity of the Earth is only about 3 percent of the recession velocity of the galaxy, which makes it insignificant.