OpenStax College Physics for AP® Courses, Chapter 23, Problem 78 (Problems & Exercises)

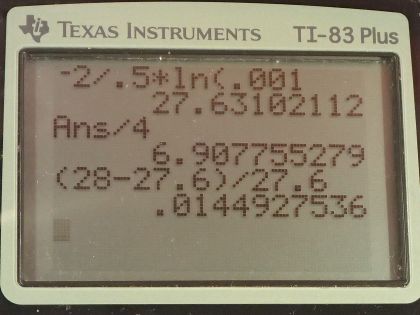
This is College Physics Answers with Shaun Dychko. We have a LR-circuit with an inductance of 2.00 henries and a resistance of 0.500 ohms and we are told that the current will fall to 0.1 percent of what it was initially so that means I equals 0.00100 times I naught. So the current is the initial current times e to the negative time divided by characteristic time constant, τ; this is for a LR-circuit where the battery has been removed and the current is decreasing with time. We can divide both sides by I naught and we get e to the t over τ equals I over I naught— we are solving for t here by the way... we want to know how long it takes for the current to fall to 0.1 percent— and this equals I over I naught, which is 0.00100. Then we take the natural logarithm of both sides and we have negative t over τ equals natural logarithm of 0.00100 and then multiply both sides by negative τ and we have t equals negative τ times natural logarithm 0.00100 and this characteristic time constant τ is the inductance divided by resistance so we substitute that in and we do that here in red. So the time then is negative 2.00 henries divided by 0.500 ohms times natural logarithm of 0.00100, which is 27.6 seconds. And part (b) is saying compare your answer to the approximate treatment using integral numbers of τ; not really sure why the question is asking this but we'll go ahead and do it anyway. First let's figure out what τ is, it's 2.00 henries divided by 0.500 ohms, which is 4.00 seconds and we have to think about what integer would we choose so let's divide these numbers and we get approximately 7. So if you wanna talk about an integer number of time constants then we would say 7 characteristic time constants. So the time then is 7 times 4.00 seconds, which is 28.0 seconds. And then part (c) asks us if this is significantly different from the exact treatment that we did in part (a). And so the percent difference is 28.0 seconds—that we got with the approximation— minus 27.6 seconds that we found using the exact methods divided by 27.6 and that's 1.4 percent... I guess we are multiplying by 100 percent here by the way. So the percent error in the approach for (a) is... we assume that the error in this number is plus or minus one of the most precise digit, which is this tenths place so that means our error is 0.1 seconds divided by 27.6 which is 0.4 percent error. So we have 1.4 percent error when using this approximate method divided by 0.4 percent error when using the exact method, which is greater by a factor of 4 so this approximate treatment does create a significant increase in the error here.