Question
A large power plant generates electricity at 12.0 kV. Its old transformer once converted the voltage to 335 kV. The secondary of this transformer is being replaced so that its output can be 750 kV for more efficient cross-country transmission on upgraded transmission lines. (a) What is the ratio of turns in the new secondary compared with the old secondary? (b) What is the ratio of new current output to old output (at 335 kV) for the same power? (c) If the upgraded transmission lines have the same resistance, what is the ratio of new line power loss to old?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 23, Problem 50 (Problems & Exercises)
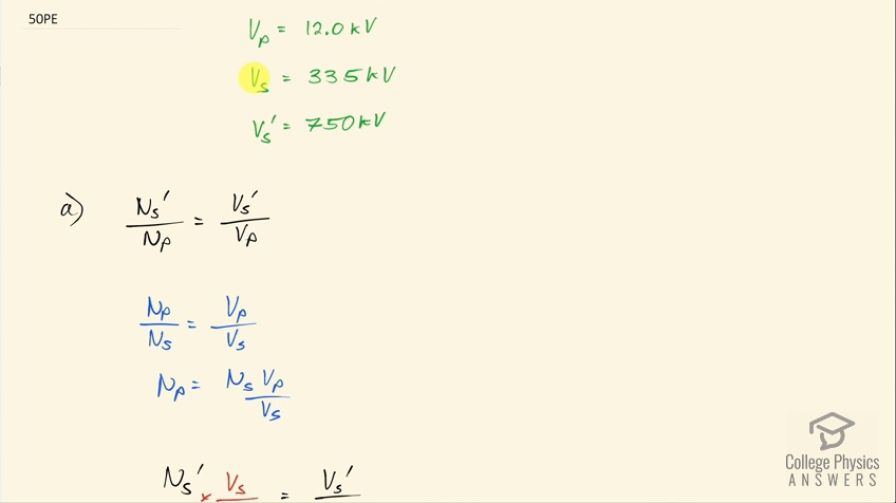
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A power plant generates electricity at 12.0 kilovolts and then sends that electricity through a step-up transformer in order to have more efficient transmission through power lines because it's more efficient to transmit at high voltage than it is at low voltage and we'll see part (c) of this question is talking about that; what's the ratio of the power lost in the lines after this higher voltage? Okay! So initially, the step-up transformer turned the voltage into 335 kilovolts but now they have replaced the secondary portion of the transformer so that it now steps up to 750 kilovolts so I called this V s prime, where prime denotes after the upgrade of the transformer. So part (a) of this question is asking what's the ratio of turns in the new secondary compared with the old secondary? So we can create an expression for the new secondary divided by the number of turns in the primary and the primary does not get a prime on it because it's the same before and after the upgrade— there's nothing done to the primary— so we'll just leave it as N p and this N s over N p or N s prime I should say over N p is the new voltage V s prime— 750 kilovolts— divided by V p. Now we want to substitute for this and replace it with N s somehow so let's create an expression with this factor with N s in it. So we have N p divided by N s is V p over V s and so the voltage in the primary divided by the original voltage in the secondary before the upgrade equals the number of turns in the primary divided by the number of turns in the secondary before the upgrade and we can solve for N p by multiplying both sides by N s and so N p is this and then we are gonna substitute now for N p and replace it with this but since we are dividing by N p and I think it's messy to have fraction within a fraction, I am gonna instead multiply by the reciprocal of this so we have N s prime multiplied by V s over N sV p. And then we want to have on the left side, N s prime over N s so we multiply both sides by V p over V s and so we have N s prime over N s then is V s prime over V s and so the new secondary voltage is 750 kilovolts divided by the old secondary voltage of 335 kilovolts and that is 2.24. And we didn't need to convert these units into volts—although we could have— because since we are taking a ratio so long as the units are the same, it's gonna be fine. So part (b) it asks for what is the ratio of the new current output to the old output? So what is I s prime—the new current output— divided by the original current output, I s, in other words? Now the power is gonna be the same in both scenarios so after the upgrade, the power in the secondary is gonna be the same as the power in the secondary before the upgrade and we can substitute for these powers so we have I s prime times V s prime equals I s times V s and then we can divide both sides by I s times V s prime and we get I s prime over I s, which is what the question's asking us for equals V s over V s prime so that's 335 kilovolts over 750 kilovolts which is 0.457. Now part (c) is asking us for the ratio of the power lost after the upgrade versus before the upgrade. So the power lost is the current that is output squared multiplied by the resistance and the power lost after the upgrade is going to be the new current I s prime squared multiplied by the same resistance so the R does not get a prime on it because we are told that the power lines have the same resistance before and after which makes sense because it's the same material. So we divide these two things and the R's cancel and we are left with I s prime over I s squared so this is the answer to part (b) basically squared which is 0.200 and this is a significant drop in the power lost after the upgrade of the voltage. Whereas the voltage was multiplied by approximately to the power lost decreases by by a factor of 0.200 so... yeah... doubling the voltage more than halves the power lost.
