Question
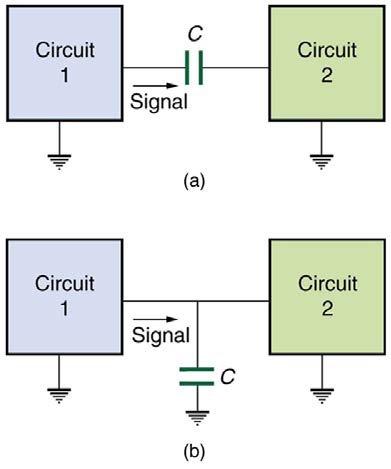
The capacitor in Figure 23.55(b) will filter high-frequency signals by shorting them to earth/ground. (a) What capacitance is needed to produce a reactance of for a 5.00 kHz signal? (b) What would its reactance be at 3.00 Hz? (c) Discuss the implications of your answers to (a) and (b).
Final Answer
- The reactance at high frequencies is very low, allowing it to short these frequencies to ground. Low frequencies experience a much higher reactance and do not flow as easily through the capacitor to ground.
Solution video
OpenStax College Physics for AP® Courses, Chapter 23, Problem 89 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
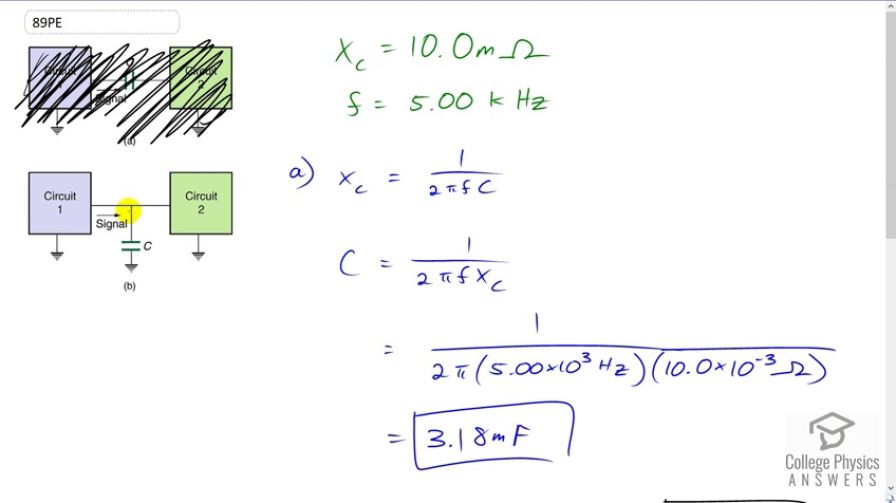
This is College Physics Answers with Shaun Dychko. This capacitor is meant to create a short circuit for high frequency signals. So, the capacitor will have a low reactance for signals that have a high frequency because here is the capacitive reactance formula. It's 1 over 2 Pi times frequency times capacitance. So, we can see that as frequency goes up, the reactance goes down. And, on the other hand, signals that are of low frequency will experience a very high reactance so they will not pass through this capacitor to ground and instead both frequency signals will continue on into circuit 2. Whereas, high frequency signals will get diverted through this nice short circuit through which it can easily flow because of the low reactance to high frequency signals and flow to ground instead of going to circuit 2. So, this is another way to make a low pass filter. So, low frequencies will pass through the filter and carry on to circuit 2. Whereas, high frequency signals will go to ground and not pass through. So, it's low pass filter. Alright. So, what is the capacitance needed in order to have a reactance of 10 milliohms so a very small reactance for a signal with frequency 5 kilohertz. So, the reactance is 1 over 2 Pi F C. And we'll solve this for C by multiplying both sides by capacitance divided by reactance. And so, we have the capacitance is 1 over 2 Pi F times reactance. So, that's 1 over 2 Pi times 5 kilohertz written as times 10 to the 3 hertz times the reactance of 10 milliohms written as times 10 to the minus 3 ohms, giving us 3.18 millifarads. Now, if the frequency was only 3 hertz, what would the reactance be? So, that will be 1 over 2 Pi times frequency times capacitance and we figured out the capacitance in part A, 0.0031831 farads. And, we're multiplying by 3 hertz here times 2 Pi, and this gives a reactance of 16.7 ohms, which is much much larger than the 10 milliohms reactance that a 5 kilohertz signal experiences. So, high reactance for low frequencies. And, part C is asking implications. Well, I think I kind of talked about that. So, reactance at high frequencies is low and so it allows it to short circuit these frequencies to ground because those signals will pass through such a low reactance. Whereas, low frequencies will not pass through it and will carry on to circuit 2.
