Question
A precision laboratory resistor is made of a coil of wire 1.50 cm in diameter and 4.00 cm long, and it has 500 turns. (a) What is its self-inductance? (b) What average emf is induced if the 12.0 A current through it is turned on in 5.00 ms (one-fourth of a cycle for 50 Hz AC)? (c) What is its inductance if it is shortened to half its length and counter- wound (two layers of 250 turns in opposite directions)?
Final Answer
- . Wires carrying current in opposite directions create magnetic fields that oppose each other. The net magnetic field will always be zero, so with no changing magnetic field there is no self-inductance.
Solution video
OpenStax College Physics for AP® Courses, Chapter 23, Problem 63 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
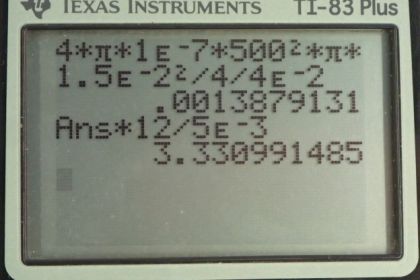
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a solenoid with a length of four centimetres and 500 turns and a diameter of one and a half centimetres and we are asked to figure out in part A, what the inductance of it would be? So, our formula for inductance for a solenoid is permeability of free space times number of turns squared times the cross-sectional area of the solenoid divided by its length. So, this is a circular solenoid, so its area would be pi times the radius squared, and we are given diameter, so we will substitute diameter divided by two in place of radius and that’s gonna be pi times diameter squared over four. Let me substitute that in for area in our formula for inductance and so the inductance will be four pi times ten to the minus seven tesla meter per amp, permeability of free space times 500 turns squared times pi times one and a half times ten to the minus two meters, that’s the diameter written in meter squared divided by four centimetres which is written as ten to the minus two meters and times four and that makes an inductance of 1.39 milli-henry. Part B asks what will the induced EMF be when it is switched on such that the current of 12 amp is the final current and it begins with zero amp so that means the change in current will be 12 amps and this happens within the time of five milli-seconds which is five times ten to the minus three seconds. So, the induced EMF will be the inductance times rate of change of current so that 1.3879 times ten to the minus three henrys, that we calculated in part A and time 12 amps divided by five milli-seconds which gives 3.33 volts. Then in part C we are told that solenoid is shortened to half of its length and the remaining wire is counter-wound backwards and so that means the wires are carrying current in opposite direction and they will produce magnetic field that are in opposite direction as well and they will cancel each other out. So, there is going to be no magnetic field inside the inductor in which case you can’t even call it an inductor anymore coz there will be no inductance because there will be no change in magnetic field.