Question
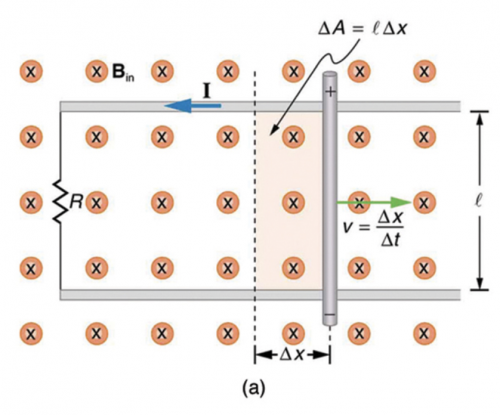
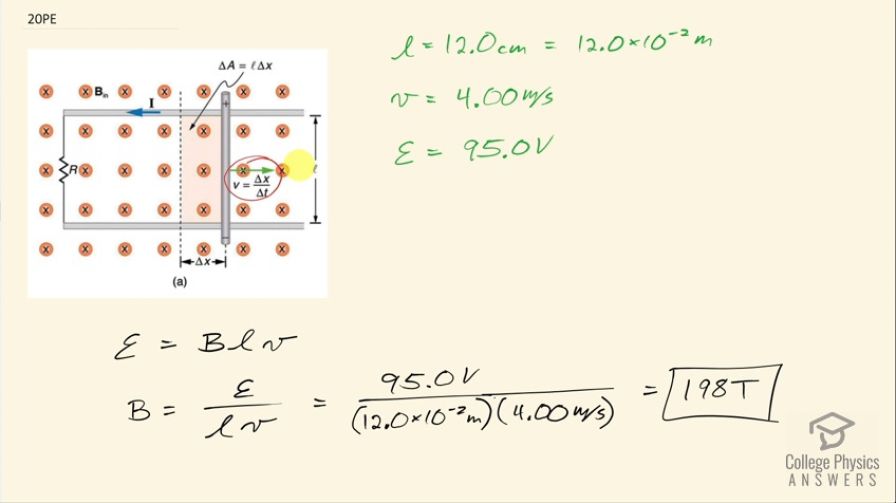
The 12.0 cm long rod in Figure 23.11 moves at 4.00 m/s. What is the strength of the magnetic field if a 95.0 V emf is induced?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 23, Problem 20 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a circuit where this metal rod is on these conducting rails and it's moving with some velocity to the right and it's increasing this enclosed area inside this loop and that's increasing the flux through this loop and so there will be an induced emf and therefore current as a result of that changing flux. So we are told that the induced emf is 95.0 volts and the speed of this rod is 4.00 meters per second and its length is 12.0 centimeters and we have to figure out what is the magnetic field strength then to account for this size voltage given these parameters. So we have a formula here but let's... I feel like deriving it so emf is the rate of change of flux in the loop there and flux is the product of the magnetic field strength and the area, assuming that they are perpendicular and so we have magnetic field strength, which stays constant so it doesn't need a Δ in front of it but the area changes so we have ΔA over Δt and then the area is this length of this rod multiplied by this other side-length here of the rail and the length of the rod isn't changing so that's just l with no Δ in front of it but the position horizontally is changing so we have Δx then over Δt and then Δx over Δt is the speed so we have Blv as a formula. So we can rearrange this to solve for B by dividing both sides by lv and then magnetic field strength then is the induced emf divided by the length of the rod times its speed. That's 95.0 volts divided by 12.0 times 10 to the minus 2 meters times 4.00 meters per second and that's 198 tesla and that's an unrealistic magnetic field strength but in any case, it is nevertheless the answer.
