Question
Prove that when , , and are not mutually perpendicular, motional EMF is given by . If is perpendicular to , then is the angle between and . If is perpendicular to , then is the angle between and .
Final Answer
Please see the solution video for illustrations.
Solution video
OpenStax College Physics for AP® Courses, Chapter 23, Problem 21 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
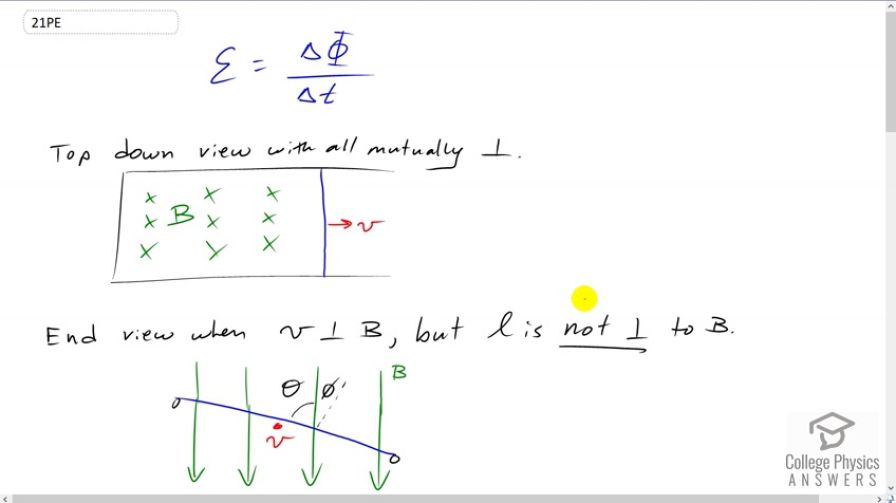
This is College Physics Answers with Shaun Dychko. Induced emf equals the rate of change of magnetic flux. And we're going to draw pictures and make a formula for the scenario where two of the three things here are not perpendicular. So right now we have: the length of the wire (is one thing), which is straight up; we have the velocity which is straight to the right, and these are perpendicular; and then we have the magnetic field into the page, which is the third thing, which is also perpendicular to the first two things. So, what happens if a couple of those things are not perpendicular? Now in the case where the length is not perpendicular to the field, we're gonna look at this picture from the end. And so, if this is your eyeball, and... I draw... maybe blue eyes, and here's a black pupil and you're looking at it from this perspective, in this direction. You look at the end and the frame is twisted. So that this part here is lower and this part here is higher up. And so this is a scenario where the length of the wire is not perpendicular to the field. And so the wire is coming straight towards you, as shown here, and the magnetic field lines are straight down. So there's this angle, phi, between the perpendicular to the plane, which is this dotted line, and the magnetic field. And the flux through the plane of the frame is going to be the component of the magnetic field, which is perpendicular, and that's going to be given by cosine of phi multiplied by magnetic field, which is along this hypotenuse. So here would be the triangle that we consider, and it's this component here that we are concerned with. This is a right angle there. So So the magnetic flux is magnetic field strength times the area of the loop times cosine of phi. So the induced emf will be the final flux, minus the initial flux divided by time. And the reason the flux is changing is because this wire is moving and increasing this area enclosed in the loop. And, so we have magnetic field and cos phi are common factors among these two terms so I factored them out. And, we're multiplying by the final area minus the initial area. And so, the final area is the length of the wire times the final distance between the wire and here. So this is x here and we have some final x f and some initial x i here. And this is -- we can factor out the common factor, L, length of the wire and so we have B L cos phi, times Delta x over t but this is the speed of the wire: the speed with which the blue wire is moving along the rails. So that's B L v cos phi. And then, the only thing left to show then is that cos phi is the same as sin of theta. So, we know that phi plus theta makes 90, because this dotted line is a perpendicular to the plane. And we're told that theta is meant to be the angle between the magnetic field and the wire, and... that's what it says here. Theta's the angle between the wire L and the magnetic field, B. So, we have phi is the 90 degrees minus theta. And cos phi then is cosine of 90 minus theta. Let's substitute this in for phi. And then we have this difference identity (trigonometric identity) for cosine of one angle minus another, so it's cos of the first times cos of the second, plus sin of the first times sin of the second angle. And cos of 90 is zero so this term disappears. And the sin of 90 is one. And so, this makes sin theta. So that makes cos phi, in this case is, the same as sin theta. And so, we have the induced emf then is B L V sin theta, which is what we wanted to show. Then, we wanna say that L and B are perpendicular, but v is not perpendicular to B. So now, we're looking at this from a side view. So, if you consider this picture here, the eyeball is now going to move and it's gonna be here. Let's get this out of the way for a second. The eyeball is gonna be looking in the plane of the page at the side of the loop. Okay. So we are looking at it like this. Now the loop is going to be tilted so that this end is gonna go down into the page, and then this end is gonna come up out of the page. So let’s put an 'x' to say this is going in and the dot says it's gonna come out, suppose. And that's the way in which the velocity will not be perpendicular to the magnetic field lines. So v is not perpendicular to B. So we have this wire moving down into the right. Now the length of the wire L is going into the page, and so it is perpendicular to the magnetic field lines which are straight down. So we have induced emf is change in flux over time, as always, and then to multiply that by the constant magnetic field strength times cosine of this angle phi to get the component of field, which is perpendicular to the plane (just as we did before), times the change in area. And, change in area is L times Delta x, as before, so we have B L cos phi Delta x over t and this is v. And, so that makes B L v cos phi, and we've already shown that cos phi equals sin theta before. So, again, we have B L v sin theta.