Question
An LC circuit consists of a 3.00 mH inductor and a capacitor. (a) Find its impedance at 60.0 Hz and
10.0 kHz. (b) Compare these values of Z with those found in Example 23.12 in which there was also a resistor.
Final Answer
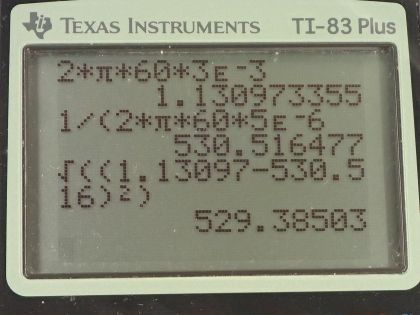
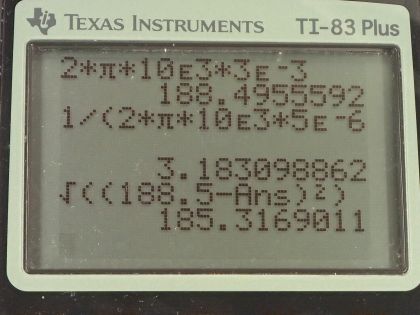
- At 60.0 Hz, the impedance is . At 10.0 kHz, the impedance is
- In comparison to example 23.12, the impedance here at 60.0 Hz differs by 0.4%, whereas at 10.0 kHz the impedance differs by 3%. These differences are small which shows that the resistor is insignificant at such low or high frequencies in comparison to the high reactances of the capacitor or inductor, respectively.
Solution video
OpenStax College Physics for AP® Courses, Chapter 23, Problem 94 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We consider a circuit with an inductor with inductance of 3.00 millihenries and a capacitor with capacitance 5.00 microfarads and these values are the same as in example [23.12] minus the resistor that's in the example. So we are gonna calculate the impedance of this circuit with only an inductor and a capacitor and then in part (b), we will compare it to what the impedance would be if the resistor was there. So impedance is the square root of the resistance squared plus the difference between the inductive reactance and the capacitive reactance squared. So the reactance is zero because there's no resistor here; the inductive reactance is 2π times frequency times the inductance and the capacitive reactance is 1 over 2π times frequency times capacitance. So at 60 hertz, the inductive reactance is 2π times 60 hertz times 3.00 times 10 to the minus 3 henries which is 1.13097 ohms and the capacitive reactance is 1 over 2π times 60.0 hertz times 5.00 times 10 to the minus 6 farads, which is 530.516 ohms. So the impedance then is the square root of this inductive reactance minus the capacitive reactance squared and that's 529 ohms. At 10.0 kilohertz, we see that the inductive reactance is gonna be much larger than it was before and the capacitive reactance would be much smaller. So the inductive reactance is 2π times 10.0 times 10 to the 3 hertz times 3.00 times 10 to the minus 3 henries 188.50 ohms and the capacitive reactance is 1 over 2π times 10.0 times 10 to the 3 hertz times 5.00 times 10 to the minus 6 farads, which is 3.1831 ohms. The impedance then is the square root of the difference between those two squared so that's 188.50 ohms minus 3.1831 ohms and then square that difference, take the square root of that and you have 185 ohms. So in example [23.12] at 60.0 hertz, the impedance was 531 and the only difference being that a resistor was also in the circuit and the percent difference is this 531 minus what we calculated here—529— and that works out to 0.4 percent difference... I guess we are multiplying by 100 percent here by the way. Okay! And then at 10.0 kilohertz, the impedance with the resistor is 190 ohms whereas it's 185 here so we have difference of 5.00 ohms divided by 185 ohms times a hundred percent is a difference of 3 percent. So these impedance's are nearly the same which means that resistance is insignificant at such high or low frequencies because at really high or really low frequencies, the reactance of the capacitor or the inductor dominates and makes the resistance small in comparison.