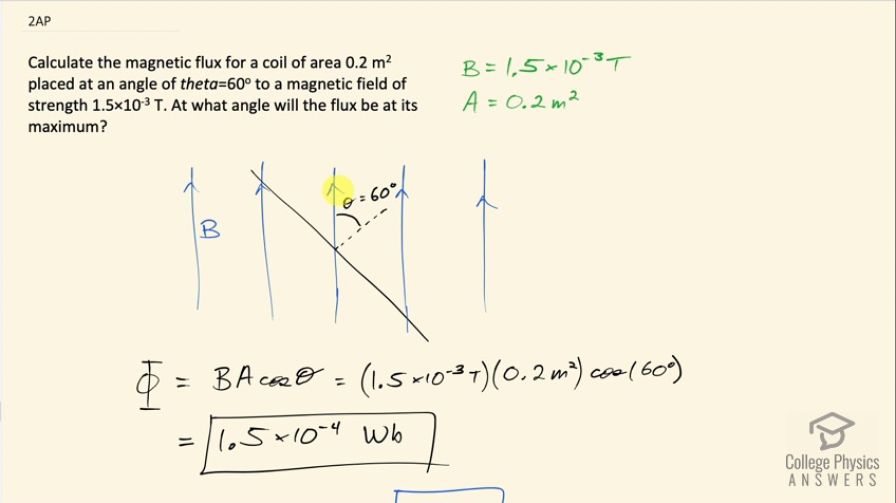
Calculate the magnetic flux for a coil of area $0.2{\text{ m}}^2$ placed at an angle of $\theta =60^{\circ }$ to a magnetic field of strength $1.5\times 10^{-3}\text{ T}$. At what angle will the flux be at its maximum?

Video Transcript

This is College Physics Answers with Shaun Dychko. A coil has an area of 0.2 square meters and it's at an angle of 60 degrees, with respect to a magnetic field. Now an angle between a coil and a field is always measured between this perpendicular to the coil and the field direction so this is the angle of 60 degrees. So the magnetic field strength is 1.5 times 10 to the minus 3 tesla and the question first of all is what is the magnetic flux through the coil? So flux is the magnetic field strength times the area of the coil times cosine of this angle between the perpendicular and the field. So that's 1.5 times 10 to the minus 3 tesla times 0.2 square meters times cos 60 and that's 1.5 times 10 to the minus 4 webers. The next question asks when does the maximum flux occur and that happens when Θ is 0 degrees because when this line is horizontal then you will have the greatest number of field lines through the coil— that's one way to think about it— flux can be thought of as how many field lines will go through the coil? Another way to think of it is that since this flux is proportional to cos of the angle, you can look at the graph of cos and it has a maximum at Θ is 0 degrees and a minimum at Θ equals 90 and so this cos Θ is maximum at Θ equals 0 so that's another reason to say the maximum flux happens at Θ equals zero.