Question
(a) Use the exact exponential treatment to find how much time is required to bring the current through an 80.0 mH inductor in series with a resistor to 99.0% of its final value, starting from zero. (b) Compare your answer to the approximate treatment using integral numbers of . (c) Discuss how significant the difference is.
Final Answer
- A 9% error is significant since it exceeds the precision of the analytical solution in part (a).
Solution video
OpenStax College Physics for AP® Courses, Chapter 23, Problem 77 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
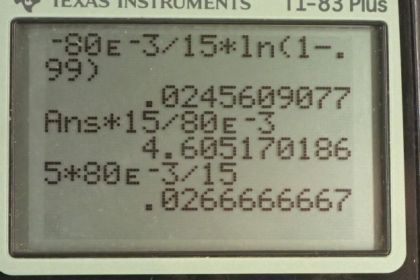
This is College Physics Answers with Shaun Dychko. In an R L circuit, we're going to figure out how much time has passed in order for the current to be 99 percent of its peak value starting from zero. So here's our formula for the current at a given time after it was zero and equals the peak current times one minus e to the negative t for time divided by Tau which is the time constant and Tau is L divided by R for an L R L circuit. Now the resistance we're told is 15 ohms and the inductance is 80 millihenry's and I divide by I naught will be 0.99 since I is meant to be 99 percent of I naught and so, we’ll substitute for Tau, first of all, and dividing by L over R is the same as multiplying by its reciprocal so that's why I have multiplied by R over L here and then we'll also divide both sides by I naught and so I over I naught equals 1 minus e to the negative t R over L and then we'll bring this to the left side by adding it to both sides. And also subtract the I over I naught from both sides. And we have e to the negative t R over L equals 1 minus I over I naught. And then we'll take the natural logarithm of both sides of this equation and on the left side we're left with the argument of the e which is negative t R over L and on the right side we have natural logarithm of 1 minus I over I naught. Then we’ll multiply both sides by negative L over R and we have the time, so time is negative L over R times natural logarithm of 1 minus I over I naught and then we plug in numbers. So we have negative 80 millihenry's written as times 10 to the minus 3 henry's divide by 15 ohms times natural logarithm of 1 minus 0.99, this gives 24.6 milliseconds will be the amount of time passing after which the current will be 99 percent of its peak then part B says use the integer method to figure out how many time constants must have passed. But to take a guess as to what integer [unclear] starting with, we'll use the answer for part A and figure out what integer is closest to the actual time. So the actual time is 24.6 milliseconds and multiply that by 15 ohms over 80 millihenry's and we end up with 4.6. So that's about five. And so if we were to do use integers multiplied by the time constant to guess what our time would be by which time the current is 99 percent of its peak, we would say, the time would be five times the time constant or five times L over R. So that's 5 times 80 times 10 to the minus 3 henry's over 15 ohms which is 26.7 milliseconds and that's quite significantly wrong. We can find the percent error by taking the difference between that and the answer we found using analytical methods in part A and then this works out to about 9 percent difference. And the reason we can say that that's significant is that 9 percent of this number. Let's suppose it's 10 percent just to make our mental calculations really easy. That'll be about 2.7. But the precision of our answer is to the tenths place. But the error in absolute terms with this, between this method and the analytical method is on the order of three milliseconds and that's an error in the ones place and so this 9 percent error is significant since it exceeds the precision of the analytical method in part A.