OpenStax College Physics for AP® Courses, Chapter 23, Problem 35 (Problems & Exercises)

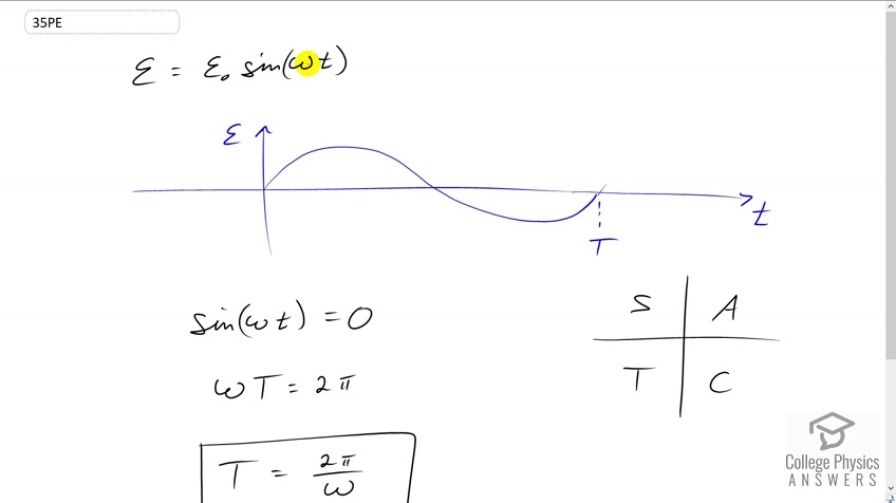
This is College Physics Answers with Shaun Dychko. We're going to show that the period of this alternating current from this generator is going to be 2 Pi divided by the angular velocity of it. Now, here's a graph of the Emf and it's a sine function. And, it starts at zero and goes through zero again and returns back to zero yet again here, and this is one full period. And so, we can see that sine of Omega T equals zero after one period is completed. And, it also equals zero when half of a period is completed. Now, there are lots of different ways to answer this question but if you consider this picture here with the four quadrants and I've put the letter C, A, S, T here to remind me in what quadrant the different trig functions are positive. So, this is cosine, all of them, sine and tangent. And, we have, you know a point on the end of a terminal arm in this picture where this is the unit circle and this might be really confusing if you've never seen this before but this point has an x coordinate equal to cosine of whatever this angle theta is here and a y coordinate equal to sine theta. And so, sine theta equals zero, the y coordinate equals zero, in other words, when this terminal arm gets to here, which is an angle of 180 degrees or better, stated as Pi radians, and then it equals 0 again when we get to 2 Pi radians here. And so, we're going to take 2 Pi to be our solution for sine of something equaling zero. And so that means that this has to be 2 Pi. So, if you put your calculator in radian mode, for example, and you take the sine of 2 Pi, you'll find that the answer is zero. And, you can also see that from this graph, I guess which I just kind of memorized that it crosses the X axis here at Pi and then again here at 2 Pi. This is just a different way of illustrating the same thing that I'm trying to illustrate with this. So, you need to think about a picture like this. You can't use your calculator directly, because if you take the inverse sine of 0, your calculator will probably give you the answer of 180 degrees or Pi radians, if you happen to have it in radian mode and even though it's true because the calculator's not going to be wrong, it's not the answer for this question because that's only half of a period has passed by the time it gets to zero for the first time and you have to take the second solution here. So, this is all to say that Omega T has to be 2 Pi because the sine of 2 Pi is zero. And that means, T is 2 Pi over Omega.