Question
(a) A car generator turns at 400 rpm when the engine is idling. Its 300-turn, 5.00 by 8.00 cm rectangular coil rotates in an adjustable magnetic field so that it can produce sufficient voltage even at low rpms. What is the field strength needed to produce a 24.0 V peak emf? (b) Discuss how this required field strength compares to those available in permanent and electromagnets.
Final Answer
- This magnetic field strength is realistic for a very strong permanent magnet. Electromagnets with superconducting coils can achieve a magnetic field strength of approximately 2 tesla.
Note: At 0:24 in the video I misspoke by saying "40 revolutions", but meant to say "400 revolutions". All of the calculations correctly use 400 revolutions.
Solution video
OpenStax College Physics for AP® Courses, Chapter 23, Problem 34 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
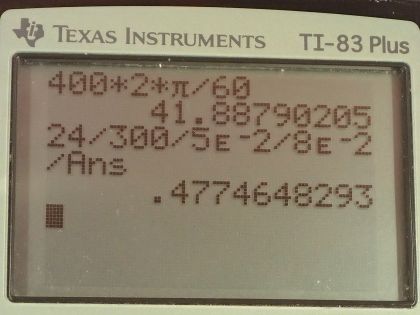
This is College Physics Answers with Shaun Dychko. We are going to figure out the magnetic field strength that's needed to produce 24.0 volts peak voltage from a generator in a car. So the generator has a coil turning with an angular velocity of 400 revolutions per minute which we convert into radians per second because we need to have mks units in our formulas—meters, kilograms and seconds— so 400 revolutions per minute gets multiplied by 2π radians in every revolution then multiply that by 1 minute for every 60 seconds, the minutes cancel so do the revolutions and we end up with 41.8879 radians per second. We are told there are 300 turns in the coil and the coil is rectangular shaped with a length of 5.00 centimeters and a width of 8.00 centimeters— both converted into meters here— and I hope there's no confusion between this letter w for 'width' which I am writing with pointy peaks versus this sort of w, which is the Greek letter ω representing angular velocity so I have tried to make them look different. Peak voltage is the number of turns multiplied by the area times the magnetic field strength times the angular velocity the area for this rectangle is its length times its width and we substitute that in place of A and then we solve for B so divide both sides by number of turns multiplied by length multiplied by width multiplied by angular velocity. So the magnetic field is adjustable apparently and we are gonna find out what it should be by dividing 24.0 volts by 300 turns times 5.00 times 10 to the minus 2 meters—length— times 8.00 times 10 to the minus 2 meters—width— times 41.8879 radians per second and the magnetic field strength should be 0.477 tesla. And part (b) asks us if this field strength is realistic and it certainly is it will be a very strong permanent magnet but since the magnetic field is adjustable, it must be an electromagnet in the car and it can also achieve the same magnetic field strength and electromagnets if they are special and made with superconducting coils, they can even achieve strengths of about 2 tesla in MRI machines. Anyway... all this to say that yes, this is achievable in the car.