Question
An RLC series circuit has a resistor, a inductor, and a 25.0 nF capacitor. (a) Find the circuit’s impedance at 500 Hz. (b) Find the circuit’s impedance at 7.50 kHz. (c) If the voltage source has , what is at each frequency? (d) What is the resonant frequency of the circuit? (e) What is at resonance?
Final Answer
- at 500 Hz: 31.9 mA
at 7.50 kHz: 312 mA
Solution video
OpenStax College Physics for AP® Courses, Chapter 23, Problem 102 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
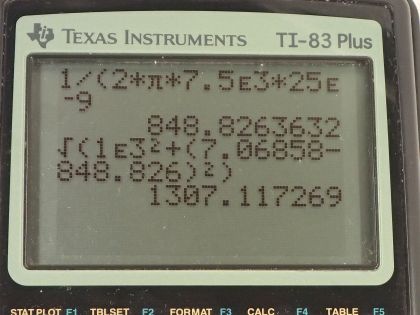
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have an RLC-circuit with a resistance of 1.00 kiloohms, which is 1.00 times 10 to the 3 ohms an inductance of 150 microhenries, which is 150 times 10 to the minus 6 henries and a capacitance of 25.0 nanofarads, which is 25.0 times 10 to the minus 9 farads. Question (a) is asking us what is the circuit's impedance given a source frequency of 500 hertz? So impedance is the square root of the resistance squared plus the inductive reactance minus the capacitive reactance squared. So the inductive reactance is 2π times frequency times inductance so that's 2π times 500 hertz times 150 times 10 to the minus 6 henries which is 0.471239 ohms. The capacitive reactance is 1 over 2π times frequency times capacitance. So that's 1 over 2π times 500 hertz times 25.0 times 10 to the minus 9 farads which is 12732.4 ohms. So we plug all of our numbers into this formula for impedance that's the square root of 1.00 times 10 to the 3—this is ohms—squared plus the inductive reactance that we found here minus the capacitive reactance and we square that difference and then take the square root of this sum of these squares and we get 12.8 kiloohms is the impedance with a frequency of 500 hertz. When the frequency is 7.50 kilohertz so we call it f prime—it's a new frequency— 7.50 times 10 to the 3 hertz the formula is the same and so let's just plug in numbers into our inductive reactance formula. So that's 2π times 7.50 times 10 to the 3 hertz times 150 times 10 to the minus 6 henries and that is 7.06858 ohms. The capacitive reactance is 1 over 2π times this new frequency times the capacitance which is 848.826 ohms and this makes the impedance the square root of 1.00 kiloohm squared plus the inductive reactance minus the capacitive reactance squared and this works out to 1.31 kiloohms. Part (c) is saying if the voltage source has an RMS voltage of 408 volts, what is the RMS current at each frequency? So at the first frequency of 500 hertz, the first RMS current then is going to be the voltage— RMS of course— divided by this impedance at 500 hertz. So that's 408 volts divided by our answer for part (a), which is 12771 ohms when you write it with more significant figures this works out to 31.9 milliamps. At 7.50 kilohertz, we have this RMS current two, which is the same RMS voltage but divided by a new impedance which is our answer from part (b) and that's 408 divided by 1307.12 ohms and that works out to 312 milliamps. Part (d) says what is the resonant frequency of the circuit? So the resonant frequency is 1 over 2π times the square root of the inductance times the capacitance. So that's 1 over 2π times square root of 150 times 10 to the minus 6 henries times 25.0 times 10 to the minus 9 farads and this is 82.2 kilohertz. And part (e) is asking what is the RMS current at resonance? So at resonance, the inductive reactance and the capacitive reactance are the same— that's what resonance means— and this difference is zero and so this works out to impedance being the same as the resistance. So the RMS current then is the RMS voltage divided just by the resistance. So that's 408 divided by 1.00 kiloohm and that's 408 milliamps.