Question
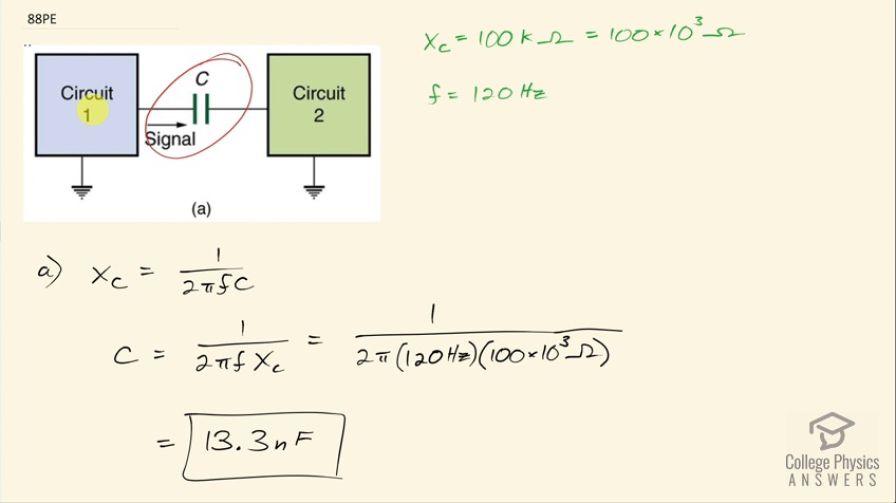
The capacitor in Figure 23.55(a) is designed to filter low- frequency signals, impeding their transmission between circuits. (a) What capacitance is needed to produce a reactance at a frequency of 120 Hz? (b) What would its reactance be at 1.00 MHz? (c) Discuss the
implications of your answers to (a) and (b).
Final Answer
- The reactance of a capacitor decreases with increasing frequency. The circuit in the figure is a high pass filter since it has such low reactance to high frequencies.
Solution video
OpenStax College Physics for AP® Courses, Chapter 23, Problem 88 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This capacitor is designed to prevent low frequency signals going from circuit 1 to circuit 2 or the other way. Anyway... between these two circuits, low frequency signals will be blocked by this capacitor because it's going to have a high reactance to low frequencies. The frequency we are told is 120 hertz and we want a capacitive reactance equal to 100 kiloohms which is 100 times 10 to the 3 ohms and what must be the capacitance in order to have this amount of reactance at this frequency? So the reactance for a capacitor is 1 over 2π times frequency times capacitance and we can solve this for C by multiplying both sides by C over capacitive reactance so C is 1 over 2πf times reactance. So that's 1 over 2π times 120 hertz times 100 times 10 to the 3 ohms and that is 13.3 nanofarads. So this capacitance—13.3 nanofarads— it will block the frequency of 120 hertz with this much reactance. Okay! Now in part (b), we are asked what is its reactance at 1.00 megahertz? So this is a new frequency— we'll call it f prime— 1.00 megahertz now, which is 1.00 times 10 to the 6 hertz and what will the new capacitive reactance be at this frequency given the same capacitance as before? So we have 1 over 2π times 1.00 times 10 to the 6 hertz times 1.32629 times 10 to the minus 8 farads— that's the same answer as part (a) but just written with more digits to avoid intermediate rounding error— and we have 12.0 ohms. So at this high frequency, the capacitor will not block high frequency signals... the resistance so to speak is only 12.0 ohms. So what this means is the reactance of a capacitor decreases with increasing frequency— we knew that from this formula— as f goes up in this denominator then the quotient should reduce... when you divide by a big number, you get a small answer in other words. And this can operate as a high pass filter; the book refers to it as a low filter so that means it blocks low frequency signals or you might also call it a high pass filter in which cases it passes through signals with a high frequency. And there we go!
