Question
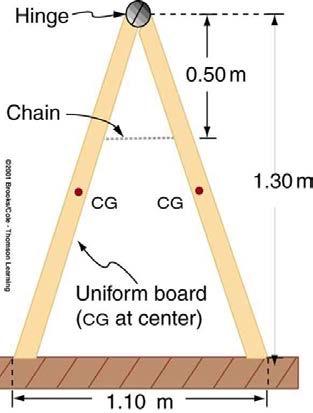
(a) What minimum coefficient of friction is needed between the legs and the ground to keep the sign in Figure 9.36 in the position shown if the chain breaks? (b) What force is exerted by each side on the hinge?
Final Answer
a)
b)
Solution video
OpenStax College Physics for AP® Courses, Chapter 9, Problem 15 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. In this problem, we're told to pretend that the chain there doesn't exist or it's broken, in which case the horizontal force on the foot of one of the sides of the sandwich board has to be provided by friction. We're going to figure out what is the coefficient of static friction that's needed, the minimum anyway that's needed to make a force that's big enough to prevent this foot from slipping. So we're going to consider just one half of the sandwich board. It's always good to take a complicated problem and try to reduce it into a smaller problem that's easier to think about. We have a bunch of forces on here. We have the normal force straight up provided by the ground, we have the friction straight to the left, we have gravity acting at the center of mass which is the geometric center of this board since we're told that it's a uniform board and the mass is distributed evenly throughout the whole length of this board. So its center of gravity is in the physical center. Then we have the hinge force which I've drawn straight to the right and I need to explain why we know that it's straight to the right. Because being a hinge it could conceivably have a component that is vertical but we'll see that it is not in this case because we'll turn our attention to this picture here. Consider this whole sandwich board as being a single point mass and the total force downwards on it would be two times the force of gravity on each side. So I have F g here representing the force of gravity on one side of the board, and so if you reduce this whole sandwich board to a dot, the total force down on it would be two times F g. And order for it to not accelerate vertically, the ground will have to provide a force upwards that's of the same magnitude. So two times this normal force in other words, which is the only force upwards on the whole thing is going to be -- well, it works out to saying that the normal force upwards has to equal the gravity downwards. Since that's the case, there can't be any upwards hinge force because this normal force is accounting for the only force that is upwards on the sandwich board as a whole. Do I need to say anymore about that? You know, if the sandwich board was not symmetrical and maybe one side was long and the other side was short, then things would get more complicated and there would be a vertical component to the hinge force for sure. We'd have to be given more information to solve it because you'd no longer be able to say that two times F n is the force upwards because there'd be force normal on the right side and there'd be force normal on the left side and they would not be equal. That means you'd have F nl plus F nr here instead of two F n but then you'd have two unknowns. So that would complicate things. But fortunately we have a symmetrical system in which case the normal force on each foot upwards is the same and so that's why we're able to say two F n. Yeah, so that's how we conclude that the normal force upwards equals gravity downwards. Since that's the case there is no place for having a vertical force on the hinge. Okay. So, well I guess I could expand on that slightly more. Let's suppose you still were to insist that there is a vertical component of the hinge force. You'd have to say that in the y direction the hinge force vertical plus the normal force would equal the gravity downwards and then you could solve for the hinge force and say that it's gravity minus normal force. But since we've just said that gravity and the normal force are equal, that makes this zero. So there is the more rigorous reason for saying vertical component of hinge force is zero. Okay, there. Now, with that out of the way, we can think about this picture and consider our three equations which we get from the two conditions for equilibrium, one being that the translational forces have to add up to zero in both directions, x and y, and then we'll say that the total torque has to add up to zero as well. So to say that the horizontal forces add up to zero is the same as saying the forces to the right equal the forces to the left. So the hinge force to the right equals the friction force to the left. I substituted coefficient of static friction multiplied by normal force in place of the friction force. Then vertically speaking we have normal force equals gravity, we've kind of already said that but just saying it again, and that is m g, mass being the mass of one side of the sandwich board. It's eight kilograms divided by two which is four kilograms. Then the total torque has to equal zero and I've taken the pivot to be at the ground but you can take it at the hinge if you like, doesn't really matter where. I chose to choose the pivot at the ground because then we have only two torques to consider. We have this due to gravity and the torque due to the hinge. If we had chosen the hinge to be the pivot, then we'd have the torque due to gravity, the torque due to friction and the torque due to the normal force and we'd have three terms to consider. So I think it's a little bit simpler to have only two. So we're taking the pivot to be at the point of contact with the ground. Okay. So we have the hinge force multiplied by its perpendicular distance to the pivot which is this 1.3 meters height of the sandwich board. That's going to be the torque which is clockwise, and that's going to equal in magnitude the torque going counter-clockwise due to the force of gravity which will have a perpendicular distance to the pivot of 1.1 meters which is the total width of the sandwich board divided by four. So 1.1 divided by two would take you to the hinge and then this center of gravity is halfway between the center point and the foot and so we divided by four to get 0.275 meters as the lever arm perpendicular for gravity. So we've equated those two things, those two torques, force of gravity is m g and then we're dividing both sides by r h the lever arm for the hinge to solve for the force of the hinge. So that's four kilograms times 9.8 newtons per kilogram, times 0.275 meters, lever arm for gravity, divided by 1.3 meters, lever arm for the hinge. That gives 8.29 newtons and that is horizontal. That's the answer for part B. The answer for part A, the coefficient of static friction, we get by rearranging this formula here and we divide both sides by F n to get that coefficient of static friction is the hinge force divided by the normal force. So that's 8.2923 newtons divided by four kilograms times 9.8 newtons per kilogram, giving a coefficient of static friction of 0.211.
