Question
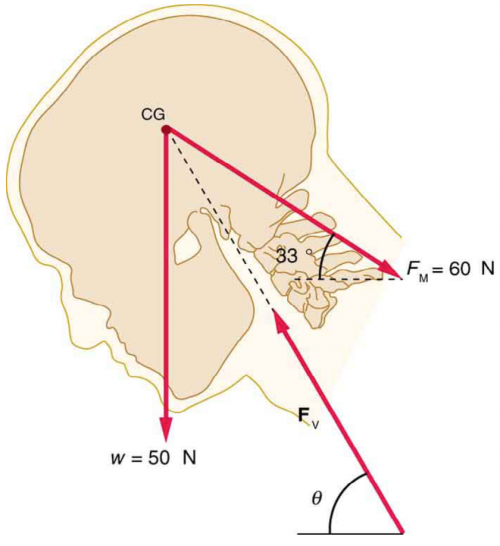
A person working at a drafting board may hold her head as shown in Figure 9.39, requiring muscle action to support the head. The three major acting forces are shown. Calculate the direction and magnitude of the force supplied by the upper vertebrae to hold the head stationary, assuming
that this force acts along a line through the center of mass as do the weight and muscle force.
Final Answer
above horizontal to the left.
Solution video
OpenStax College Physics for AP® Courses, Chapter 9, Problem 30 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
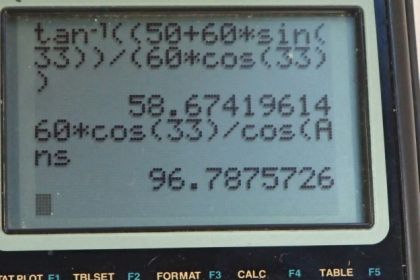
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The weight of the head is straight down there's this force due to some neck muscles which are acting in an angle of 33 degrees above horizontal and then there's this force of the upper vertebrae which we assume is acting along this line through the center of gravity at some angle Θ with respect to horizontal and our job is to find this angle Θ and this force due to the vertebrae. So the horizontal forces have to add up to zero which is to say that the forces to the left have to equal the forces to the right so weight does not play a part in that since it is entirely up and down and so we have F V times cosine Θ is the horizontal component of this force due to the vertebrae and that's going to equal the force due to this muscle multiplied by cos 33 degrees. And that's all we can say in this equation because there are two unknowns and so we can't solve for either of them until we have a second equation and we get that by thinking about the vertical direction. So the total up forces have to equal the total down forces so that's F V times sin Θ so this is F V y-component here— it's the opposite leg of this right triangle so we use sin Θ multiplied by the hypotenuse to find it— and that equals the weight downwards plus the muscle force multiplied by sin 33. Now we can rearrange this equation from the x-direction to solve for F V and it's F M cos 33 over cos Θ and so we divided both sides by cos Θ to do that and then that's useful because then we can look at this equation and replace the unknown F V with this expression containing the only remaining unknown which is Θ. So replacing F V with F M cos 33 over cos Θ multiplied by the remaining sin Θ equals w plus F M sin 33 and sin Θ divided by cos Θ can be replaced with the trigonometric identity tangent Θ and so I did that and then I also divided both sides by F M cos 33. And so we have tan Θ is w plus F M sin 33 divided by F M cos 33 so Θ is the inverse tan of all that. And so that's inverse tan of 50 newtons—weight— plus 60 newtons—force due to the muscle— times sin 33 divided by 60 newtons times cos 33 which is 59 degrees. Now the magnitude of the force due to the vertebrae can be found using this equation here where we now know Θ so we can replace it and so we have 60 newtons times cos 33 divided by cos of 58.674 degrees— that's this number with more decimals— and that is 97 newtons. So the force due to the vertebrae is 97 newtons, 59 degrees above horizontal to the left.