Question
We analyzed the biceps muscle example with the angle between forearm and upper arm set at . Using the same numbers as in Example 9.4, find the force exerted by the biceps muscle when the angle is and the forearm is in a downward position.
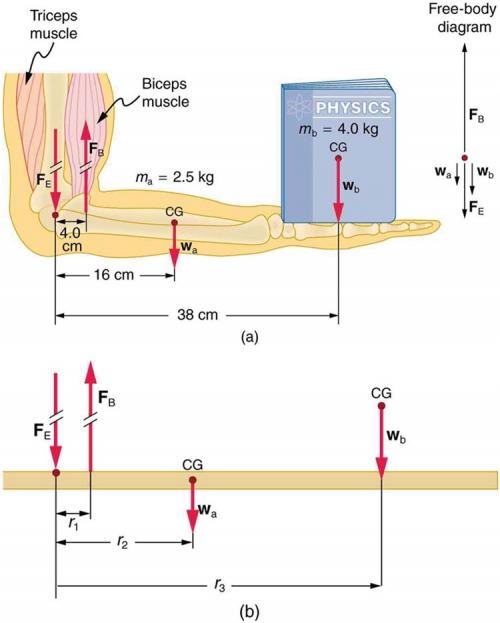
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 9, Problem 31 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
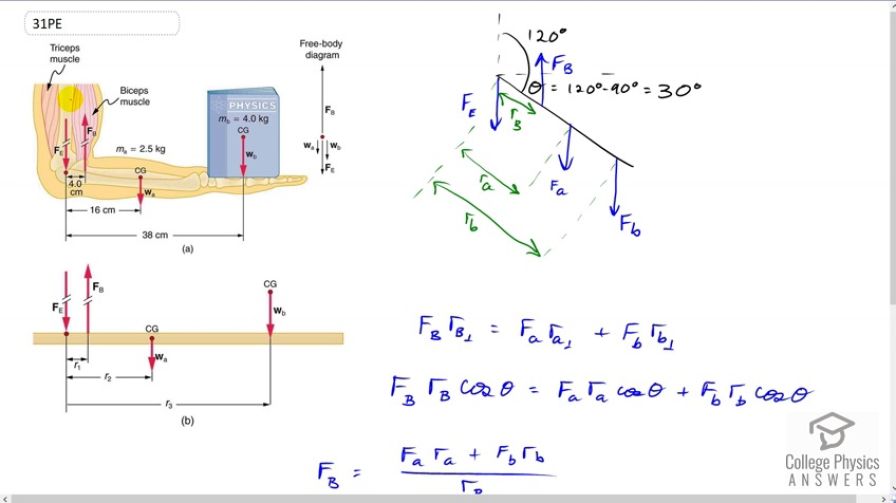
This is College Physics Answers with Shaun Dychko. We're going to re-do this question that we've done before in an example but with the angle of between the arm and the bicep going to be 120 degrees. So the hand is down here and the book is on the hand down here. Okay. So, the torques that are going counter-clockwise of which there is only one due to the bicep has to equal the total torque going clockwise. We're assuming the pivot is at the elbow here and so the force exerted on the elbow has no term in our torque formula because its lever arm is zero. We're multiplying each of these forces by the perpendicular component of this distance to the elbow. So, this angle theta which is between the horizontal and the arm is going to be 120 minus 90, and that gives 30 degrees. So the horizontal component of each of these lengths here is going to be the hypotenuse which is the length, multiplied by cosine of thirty. If we consider this triangle for the bicep first of all, it's this triangle here where this is r b and this is r b perpendicular that we want to know, perpendicular to the force. This angle here is 30, that's a right triangle, and so we multiply the hypotenuse by cosine of 30 to get the adjacent. So we substitute that into each of these terms here and we have F b times r b cos theta equals force of weight on the arm, multiplied by the distance from the center of mass of the arm to the elbow, times cos theta, plus force of weight on the book, times the distance from the book to the elbow, multiplied by cos theta. But this is cos theta is a factor on every term and so we can divide both sides by cos theta and it disappears. Then also divide both sides by r b and you solve for the force due to the bicep. So then we plug in numbers. We have two and a half kilograms times 9.81 newtons per kilogram, this is the force of the weight of the arm, multiplied by its 16 centimeter distance to the elbow. I can use centimeters here because since we have centimeters on top and centimeters on the bottom, those units are going to cancel. It doesn't matter what the units are so long as they are the same on top and bottom. You could convert them to meters if you prefer. Then add to this the four kilogram mass of the book times 9.81 times 38 centimeters from the hand to the elbow, divided by four centimeters lever arm of the bicep, or you know, not quite the lever arm technically but it's the distance from where the bicep attaches to the arm bone, the radius or the ulna. Anyway this works out to 471 newtons which is the same as we had in the example by the way. The angle didn't make any difference because it canceled.
