Question
Suppose you needed to raise a 250-kg mower a distance of 6.0 cm above the ground to change a tire. If you had a 2.0-m long lever, where would you place the fulcrum if your force was limited to 300 N?
Final Answer
from where the 300N force is applied.
Solution video
OpenStax College Physics for AP® Courses, Chapter 9, Problem 20 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
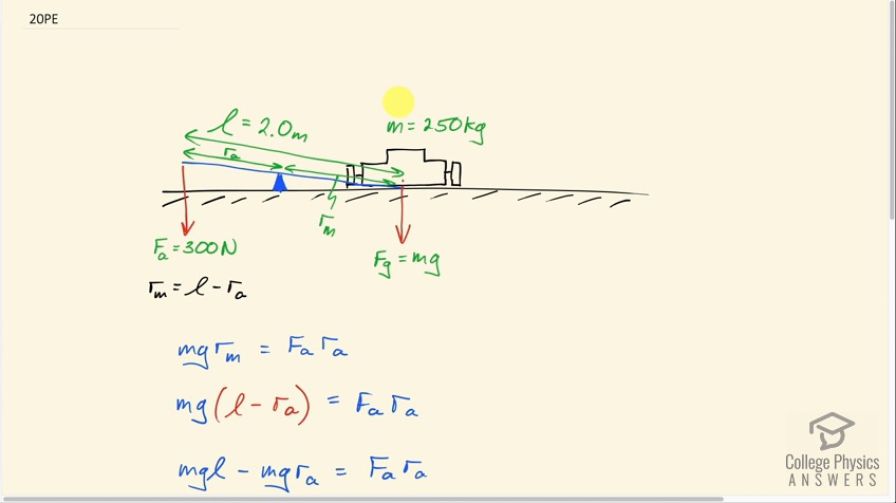
This is College Physics Answers with Shaun Dychko. This lever is placed right under the middle of the mower so that it is going to be lifting the mower straight up, in which case, the mower has a center of gravity right in the middle applying a force straight down on the lever and that force is its mass times, you know, gravitational field straight, mg. The mass is 250 kilograms; our job is to figure out where should this fulcrum go such that this 300 newton applied force is enough to lift up the mower given this lever is 2.0 meters long. So we have a lever arm for the applied force r a and we don't know what that is but we have labeled it anyway and then this is the lever arm for the mower, subscript m for mower, and this distance here from the fulcrum to the mower is gonna be the full length of the lever minus the lever arm of the applied force— so we say that here— and we are gonna say that the torque due to the mower which is... which is clockwise is equal to the counter-clockwise torque due to the applied force and then substitute in l minus r a in place of r m and distribute the mg into the brackets here: we have mgl minus mgr a equals F a times r a and our job is to collect the r a terms on the same side because we want to isolate and solve for this lever arm for the applied force. And so we'll add mgr a to both sides and then switch the sides around and we have this line here factor out the common factor r a and so we are left with r a times F a plus mg equals mgl and then divide both sides by this bracket. So we have the lever arm for the applied force is mass of the mower times g times the length of the lever divided by the applied force plus mg. So that's 250 kilograms times 9.80 newtons per kilogram times 2.0 meters divided by 300 newtons plus 250 kilograms times 9.80 giving us 1.8 meters is the position of the fulcrum then from where the 300 newton force is applied. So we need this r a to be 1.8 meters so the fulcrum is actually way over here and there we go!
