Question
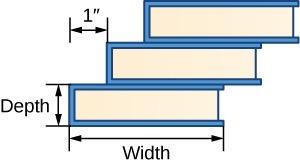
A group of students is stacking a set of identical books, each one overhanging the one below it by 1 inch. They would like to estimate how many books they could place on top of each other before the stack tipped. What information below would they need to know to make this calculation?
- The mass of each book
- The width of each book
- The depth of each book
- I only
- I and II only
- I and III only
- II only
- I, II, and III
Final Answer
. The number of books that can be stacked equals the width of each book in inches. See the solution video for an explanation.
Answer: (d).
Solution video
OpenStax College Physics for AP® Courses, Chapter 9, Problem 5 (Test Prep for AP® Courses)

vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. I'm going to derive an expression to show that the number of books you can stack equals the number of inches wide each book is. So we're going to show why the answer is D for this question, why only the width of each book is what matters. So, when you're stacking them up these books on top will fall when the center of mass of these stacked books is positioned beyond the edge of the bottom book because at that point once you have enough books stacked on top here, and the center of mass is here, say -- let's suppose there's three stacked on top, the center of mass was here, then it would have some perpendicular component to its lever arm on the right hand side of the edge of the book. Here's the pivot and this would exert a clockwise torque and it would cause the books to fall. So as long as the center of mass is actually on the left side of this pivot, then in this case gravity is exerting a counter-clockwise torque and it keeps the books stacked up and not falling. So, we're going to calculate where the center of mass is based on the number of books that are stacked and then create an expression for in general, how many books could be stacked. So let's review center of mass first of all. When you have multiple objects, you have the center of mass of the first object multiplied by its mass, plus the center of mass of the second object multiplied by its mass, all divided by the total mass. But in this case, since all the books are the same mass, we can forget about writing subscripts on the end and factor it out. Then on the denominator as well, we have m and I've written n minus one here for this specific question to say that it's the number of books minus one, is the number of masses on the bottom because we're only going to be including the books that are stacked on top in this calculation for center of mass. So when there are three books, there's only two books that we need to consider. Like when there are three books in total including the one on the bottom, there are only two books that we need to include in our calculation for center of mass. So, the m's cancel and so this is the formula that I'm using to get each of these rows in this table here. So when there are two books, there is only -- n is two, and the center of mass will be the middle of this particular book plus one, plus one inch there. So we have the width divided by two because it's a uniform book and so the center of mass of each book is in the middle of the book, plus this one inch and -- so yeah, that's the center of mass of the stack above the first when there are two books. Then when there are three books, we need to take basically the average of the center of mass positions of this book and this book. So the first book again has w over two plus one as its position and the second book is w over two plus two inches because there is another inch here. All that gets divided by the number of stacked books which is two, which is the total number of books, being three minus one. Then with four books, we are adding another term here, w over two plus three inches divided by three. We can see a pattern now that we can generalize. So we have the center of mass is going to be the number of books minus one, multiplied by w over two because when there are four books, you can see w over two is a factor that appears three times and so we want to multiply w over two by three when there are four books. So if we go, the number of books being four say, minus one, that gives us three and multiply by w over two. That's an expression accounting for the w over two factor. Then we have this arithmetic series of one plus two plus three plus so on, and the sum of an arithmetic series is the first term plus the last term multiplied by the number of terms divided by two. That's just a formula -- well, we could derive it but that's a different topic. So in this case, we have the first term is always one, plus the last term is going to be the number of books minus one, and then we multiply that by the number of terms which will be the number of books minus one, again. So when there are four books, there are three terms, one, two, three, and then divide that by two because that's what the formula says. We can substitute that in here and all that gets divided by the number of books minus one as we said up here. This works out to wover two plus n over two. This one half and the negative one half cancel. Now the books fall when the center of mass is positioned at the width of the bottom book. At least that's where they, you know -- just slightly beyond that is when they fall. So we'll have basically, we'll have falling when w over two plus n over two equals the width. Subtract w over two from both sides you get n over two equals w over two. In other words, n equals w. So, this shows that the number of books you can stack depends only on the width. The answer is D.