Question
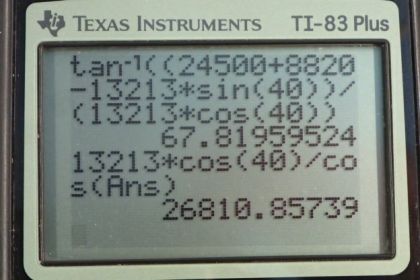
Suppose a 900-kg car is on the bridge in Figure 9.35 with its center of mass halfway between the hinges and the cable attachments. (The bridge is supported by the cables and hinges only.) (a) Find the force in the cables. (b) Find the direction and magnitude of the force exerted by the hinges on the bridge.
Final Answer
a)
b) ,
Solution video
OpenStax College Physics for AP® Courses, Chapter 9, Problem 13 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. There is a car in the middle of this bridge at a position which is 4.5 meters from the pivot which we’ll take to be this hinge here, and we get 4.5 meters by taking the total length of the bridge, seven and a half meters from the center of gravity to this end, plus the one and a half meters between the center of gravity and the hinge, and divide that by two. We have the level arm for this tension force is going to be seven and a half plus 1.5 so that’s going to be nine meters there. We’re going to equate the x direction forces, this hinge is going to exert a force to the right in the x direction and that component will be the hinge force multiplied by cosine of this angle because we’re going to be finding the adjacent leg of this yellow triangle. That will equal the force to the left due to tension which will be the tension force multiplied by cos 40 so that gives that component here. We can’t solve that equation because we don’t know any of these three things here, F, theta or T and so we’ll have to turn our attention to a different equation which we’ll get by considering the y direction. So the component of the hinge force that is vertical plus the component of tension which is vertical, both of those are going up, and they will equal the total down forces which are the weight of the bridge plus the force of gravity on the car. We’ve calculated the force of gravity on the car is mass of the car times g that results in 8820 newtons and the weight of the bridge is mass of the bridge times g which is 24500 newtons. But this equation we also can’t solve because again there are three unknowns, and whenever you have three unknowns, you need to have three equations to solve for them. So our third equation comes from torque. And so we have the total clockwise torque due to gravity and the car are going to equal the counter-clockwise torque which is due to the tension force and all of these are above the pivot at the hinge here. So the weight of the bridge multiplied by the level arm of the bridge plus the weight of the car multiplied by the car’s level arm is going to equal the y component of tension multiplied by its level arm of nine meters, so that’s T times sine of 40, that’s the y component of tension, multiplied by nine, and then we divide both sides by sin 40 times nine, and this gives us the tension force. So that’s 24500 newtons weight of the bridge multiplied by the bridge’s 1.5 meters distance between its center of mass and the pivot, plus the weight of the car 8820 newtons times 4.5 meters from the pivot, divided by sin 40 times nine, and that gives us this number here. Now you have to realize that a bridge is usually made with a cable on each side of it and then people or cars or bicycles or whatever can go down the middle, the bridge would twist if it didn’t have a cable on both sides, and so there are two cables to consider even though you can’t really see them in this side picture. So the tension in each cable is going to be this total tension divided by two, so this works out to 6610 newtons of tension in each cable. Then, we look at equation one and solve it for F by dividing both sides by cos theta and so it’s T times cos 40 divided by cos theta, and we do that because we want to substitute for F in equation two. Now that we know T, we can substitute the number for that but we still have an equation here that has theta and F, both of which we don’t know and so we’ll replace one of them with stuff that we do know. So we’re replacing the F with this expression T cos 40 over cos theta, so that’s written in red here, that substitution, otherwise I’ve copied equation two. And sin theta over cos theta is a trigonometric identity and it’s tan theta. So we can replace all that with tan theta and so we have T cos 40 times tan theta equals the weight of the bridge plus the weight of the car minus this term here which we subtracted from both sides, then we can divide both sides by T cos 40 to solve for tan theta. Then take the inverse tangent of both sides to get theta, so theta is the inverse tangent of the weight of the bridge plus the weight of the car minus the tension in the cable, that’s the total tension, times sin 40 divided by total tension times cos 40, and this works out to 67.8 degrees. Then, we can put that angle into this equation here, into the denominator, so we know T and we know theta to solve for F. So F is going to be the total tension force of 13213 newtons times cos 40 divided by cosine of 67.8196 degrees, this gives 26800 newtons is the force exerted by the hinge. I guess these parts here are part b.