Question
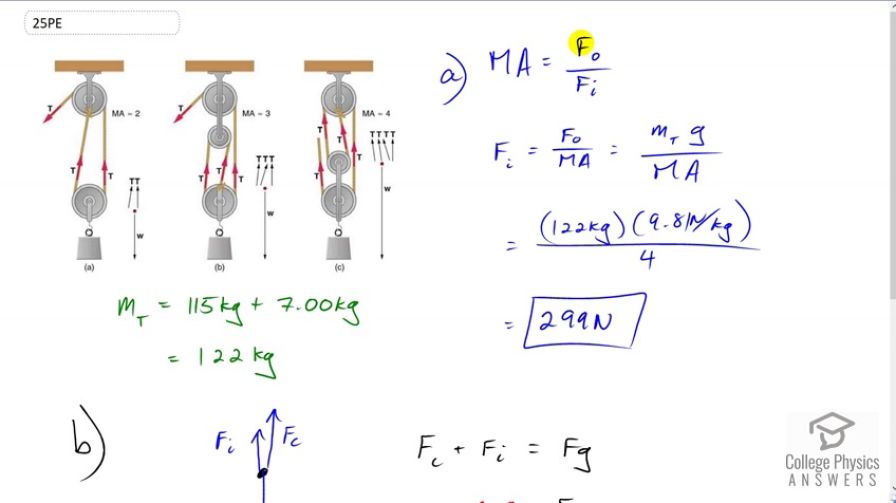
Repeat Exercise 9.24 for the pulley shown in Figure 9.27(c), assuming you pull straight up on the rope. The pulley system's mass is 7.00 kg.
Exercise 9.24
If you used an ideal pulley of the type shown in Figure 9.27(a) to support a car engine of mass 115 kg, (a) What would be the tension in the rope? (b) What force must the ceiling supply, assuming you pull straight down on the rope?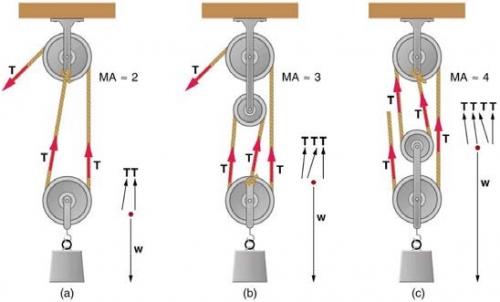
Final Answer
a)
b)
Solution video
OpenStax College Physics for AP® Courses, Chapter 9, Problem 25 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We’re given the mechanical advantage of this pulley system in part c is four. We know mechanical advantage is the output force divided by the input force, so we’ll solve this for the input force by multiplying both sides by Fi over MA. Then we get the input force is the output force divided by mechanical advantage. So the output force has to be the total weight of the pulley system and the engine hanging off of it, so that’s 115 kilograms plus seven kilograms which is 122 kilograms times 9.81, and all that is divided by the mechanical advantage of four, to give an input force required of 299 newtons. And then part b asks us to find out what is the force exerted by the ceiling on the system. Well let’s first of all redraw the system as a single dot and consider the forces that are on that dot. There is gravity downwards due to the weight of the system and the engine, then there’s the force of the ceiling upwards which we’re going to find, and the way this pulley system is constructed, there’s also one force upwards which is the input force. All these other Ts inside here, these tensions, are forces that are internal to the system and they are not externally applied. So the force of the ceiling plus the input force upwards equals the total force of gravity downwards, and we’ll subtract Fi from both sides and also substitute mg in place of Fg, and we get the force applied by the ceiling, 122 kilograms times 9.81 newtons per kilogram minus 299.205 newtons input force, giving us 898 newtons is the force applied by the ceiling.
