Question
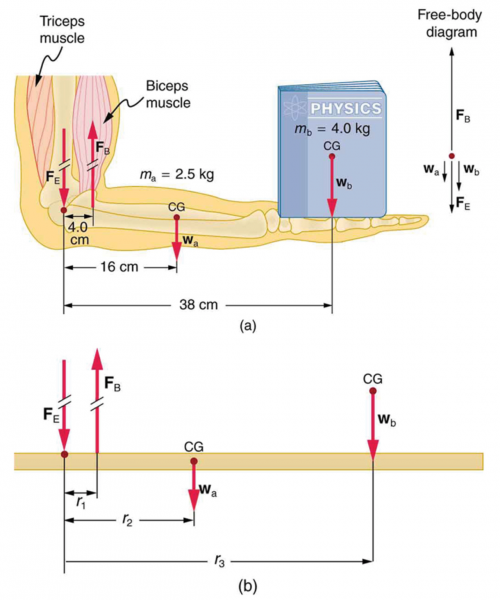
Verify that the force in the elbow joint in Example 9.4 is 407 N, as stated in the text.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 9, Problem 26 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This arm is holding a book and the arm has a mass of 2.5 kilograms, the book has a mass of 4.0 kilograms and the positions are as shown here: the hand is 38.0 centimeters from the elbow joint and the center of mass of the arm is 16.0 centimeters from the elbow joint and the bicep articulates here 4.0 centimeters from the elbow joint and the bicep is exerting a force upwards and the elbow joint and the weight of the arm and the book weight are all downwards and our job is to figure out what is this force on the elbow joint? due to the humerus bone here. So here's a simplified picture just showing this model that has a single plank with a bunch of forces on it and we are going to use the first condition of equilibrium which is to say that the total vertical forces have to equal zero so we have the forces upwards of which there's only one— the force due to the bicep— equals the total forces downwards— that's the force on the elbow joint plus the weight of the arm plus the weight of the book. And then there are two things we don't know so that means we need to have a second equation to solve for them and we are gonna say the second condition of equilibrium is that the total clockwise torque has to equal the total counter-clockwise torque and so we have two clockwise torques taking the pivot to be at the elbow here and so we have the weight of the arm multiplied by the arm's lever arm—r 2— plus the weight of the book multiplied by the book's lever arm—r 3— equals the counter-clockwise torque due to the bicep force which is F B multiplied by r 1. And we can solve this for F B by dividing both sides by r 1 and then make a substitution for F B in this first condition of equilibrium so we replace F B with this whole expression that we figured out using the torque business and now we have an equation with only one unknown, F E. So we can solve for it by subtracting m ag and m bg from both sides and we are left with this line here. The force on the elbow is g multiplied by m ar 2 plus m br 3 all over r 1 minus m ag minus m bg. So we plug in numbers from this picture here so we have 9.80 newtons per kilogram times 2.5 kilograms—mass of the arm— multiplied by—its lever arm—16.0 centimeters and then leaving the units as centimeters which... you know, is a bit dangerous to do you have to do it and if you have to think about why you are keeping the units as centimeters and not changing them to meters, you have to have a good reason and the good reason here is that the units for the length in the numerator will be centimeters and the same units will be in the denominator of this fraction so the centimeters are going to cancel, in other words. So the only important thing is that the length units are the same as they are, they are both centimeters and so that's good; you could change them both to meters and that would be fine too but that's just a little extra work. Okay! So we add to this 4.0 kilogram— mass of the book— times—its lever arm of—38 centimeters and divide all that by 4.0 centimeters— the lever arm of the bicep muscle— and then take from that 2.5 kilograms times 9.8 minus 4.0 kilograms times 9.8 and we have 407 newtons is the force on the elbow joint.
