Question
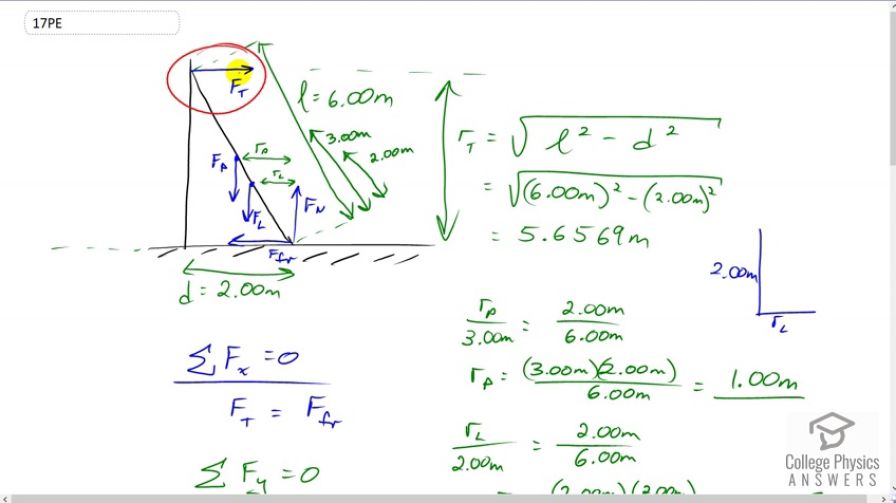
To get up on the roof, a person (mass 70.0 kg) places a 6.00-m aluminum ladder (mass 10.0 kg) against the house on a concrete pad with the base of the ladder 2.00 m from the house. The ladder rests against a plastic rain gutter, which we can assume to be frictionless. The center of mass of the ladder is 2 m from the bottom. The person is standing 3 m from the bottom. What are the magnitudes of the forces on the ladder at the top and bottom?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 9, Problem 17 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a ladder propped up against a frictionless wall and we need to figure out what is the force exerted by the wall at the top of the ladder, and also the force exerted on the bottom of the ladder which has two components. It has a normal force straight upwards and a friction force to the left. Now being told that the wall is a frictionless, you know it says the eaves trough is frictionless or rain gutter I should say, is frictionless. That means there is no vertical component to this force. It has to be entirely horizontal because it would require friction to exert a force upwards or downwards. So well there's a bunch of other things on here relating to torque but let's stick with the easy stuff first. We'll say that the forces horizontally have to balance out and so they have to total zero. So the forces to the right have to equal the forces to the left. There is one force to the right, that's the force at the top of the ladder and that has to equal the friction force at the bottom of the ladder going to the left. In the y direction we have the forces upwards have to equal the total forces downwards. So we have the normal force up has to equal the force of gravity on the person plus the force of gravity on the ladder downwards. Then we'll think about torque. So we'll choose the pivot to be at the ground because that reduces the number of terms in our torque equation since we'll have only three torques due to each of these three forces. Whereas if we chose the pivot to be at the top, we would have four different torques to consider. So it just makes things a little bit easier to choose it at the bottom. But either one would work. So, we need to know what the perpendicular distances are between each of these three forces F t, F p, and F l, to the pivot at the bottom. So the lever arm for the force at the top is going to be this vertical distance and we're told that the ladder is six meters long and the base is two meters away from the wall. So this leg here will be the square root of the hypotenuse which is six meters, squared, minus the base squared. So the square root of six squared minus two squared and that gives 5.6569 meters and that's going to be the perpendicular distance from this force at the top to the pivot. Now to get the perpendicular distance r p, this is the lever arm of the force on the person, and that is the horizontal leg of this triangle here in yellow. This yellow triangle is similar to this ladder triangle in blue, similar meaning that all the angles are the same. That means the ratio of corresponding sides is equal. So when we take the base of this yellow triangle r p which we want to find, and divide it by its hypotenuse which is three meters, since we're told that the person is three meters above the bottom of the ladder and we can assume that that means along the ladder, so that's three meters in this diagonal here. So r p divided by three meters is going to equal the base of the blue triangle, two meters, divided by its hypotenuse of six meters. Then multiply both sides by three here to solve for r p. We have it's three meters times two over six which is one meter. Then the lever arm for the force of gravity on the ladder, we're told that the center of gravity of the ladder is two meters above the ladder's bottom. So that divided by two, so that's r l divided by two, that's the base divided by its hypotenuse is going to equal the same ratio as before, the ladder triangle base two meters, divided by the length of the ladder, six meters. That's going to work out to 0.667 meters is the lever arm for the ladder force. So we have that F t the force at the top of the ladder, times the lever arm at the top of the ladder, that's the torque going clockwise, equals the total counter-clockwise torques which is force of gravity on the person times its lever arm plus the force of gravity on the ladder times the ladder's lever arm substituting m g in for each of these gravity forces and factoring out the common factor g, we get g times mass of the person times r p plus mass of the ladder times r l. Then we can divide both sides by the lever arm of the force at the top and then we solve for F t. So the force at the top is g times m p r p plus m l r l over r t. That is 9.81 newtons per kilogram times 70 kilograms mass of the person, times one meter lever arm, plus ten kilograms mass of the ladder, times 0.6667 meters lever arm, divided by 5.6569 meters lever arm of the force at the top. This gives 133 newtons. So the force of friction is equal to that. Well I've written down the unrounded numbers since we're going to use this in a subsequent calculation to figure out the resultant force at the base of the ladder. So I've written 132.953 newtons and the normal forces upwards, is equal to the total force of gravity downwards which is g times the sum of the masses of the person and ladder. So that's 9.81 times 70 plus 10 and that gives 784.8 newtons. The force at the bottom of the ladder is going to be the resultant of this normal force and force of friction. So these being the two components of this resultant which is like this or so. It's not exactly along the ladder. To figure out the angle we'd have to take the inverse tangent of force of friction divided by F n or the other way around, F n divided by force of friction. But it doesn't ask us for the angle. It says just what is the magnitude of the force. So, we take the square root of the friction force squared plus the normal force squared. So the square root of 132.953 newtons squared plus 784.8 newtons squared and this gives 796 newtons is the force at the base of the ladder.

