Question
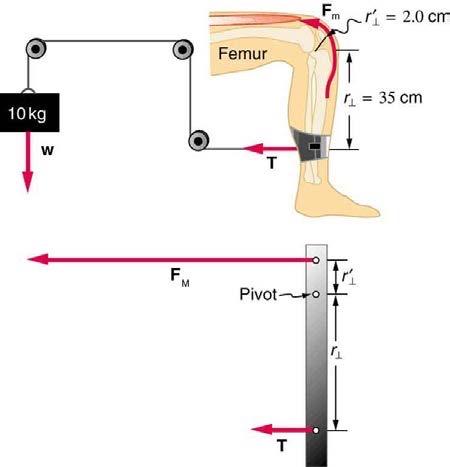
A device for exercising the upper leg muscle is shown in Figure 9.40, together with a schematic representation of an equivalent lever system. Calculate the force exerted by the upper leg muscle to lift the mass at a constant speed. Explicitly show how you follow the steps in the Problem- Solving Strategy for static equilibrium in Applications of Statistics, Including Problem-Solving Strategies.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 9, Problem 29 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
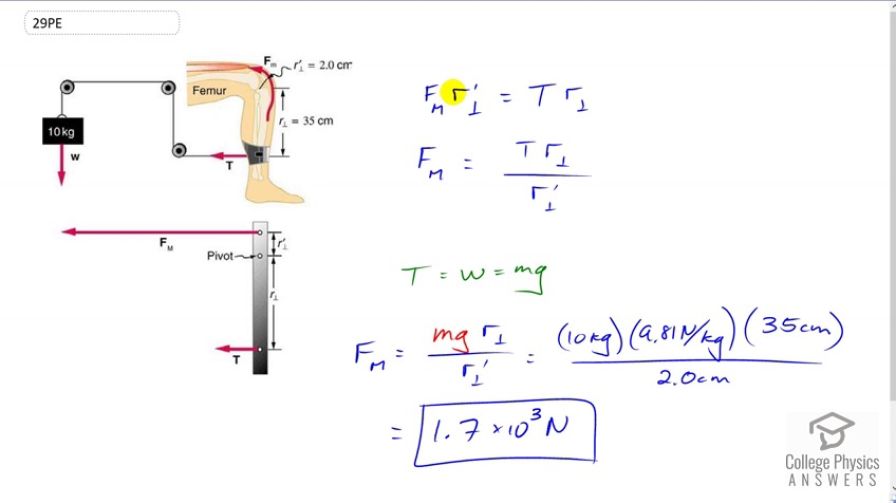
This is College Physics Answers with Shaun Dychko. The torque exerted by the upper leg muscle is going to be the force that it exerts FM multiplied by r prime perpendicular, that’s the level arm of the leg muscle. That’s going to equal this tension in this cable that’s connected to the weight, multiplied by its level arm of 35 centimeters, and we’ll divide both sides by r prime perpendicular to solve for the force due to the muscle. We need to know what this tension force is then. Now the tension will be the same throughout the cable, and so it’s also going to be a force directly upwards on this weight. The weight has a mass of ten kilograms and so we’ll substitute that mass multiplied by the gravitational field strength in for T. So the force due to the muscle is mg r perpendicular over r prime perpendicular, so that’s ten kilograms times 9.81 newtons per kilogram times 35 centimeters divided by two centimeters. Notice that there is no need to convert the units here, normally we would have meters, kilograms and seconds in our calculations, but in this particular case since we’re dividing the lengths, the units will cancel and so the only important thing is that they are the same units and they are, both centimeters here so that’s why it’s okay. We get 1.7 times ten to the three newtons is the force exerted by the muscle.
