Question
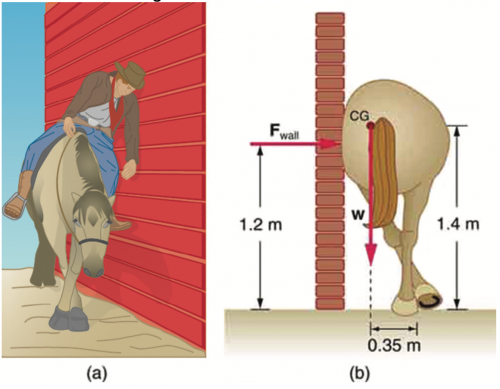
(a) Calculate the magnitude and direction of the force on each foot of the horse in Figure 9.30 (two are on the ground), assuming the center of mass of the horse is midway between the feet. The total mass of the horse and rider is 500kg. (b) What is the minimum coefficient of friction between the hooves and ground? Note that the force exerted by the wall is horizontal.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 9, Problem 8 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
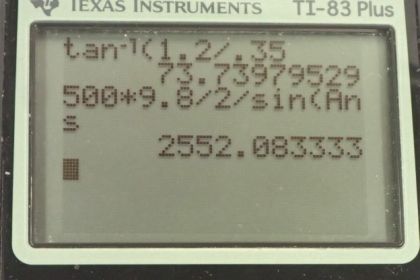
Calculator Screenshots
Video Transcript
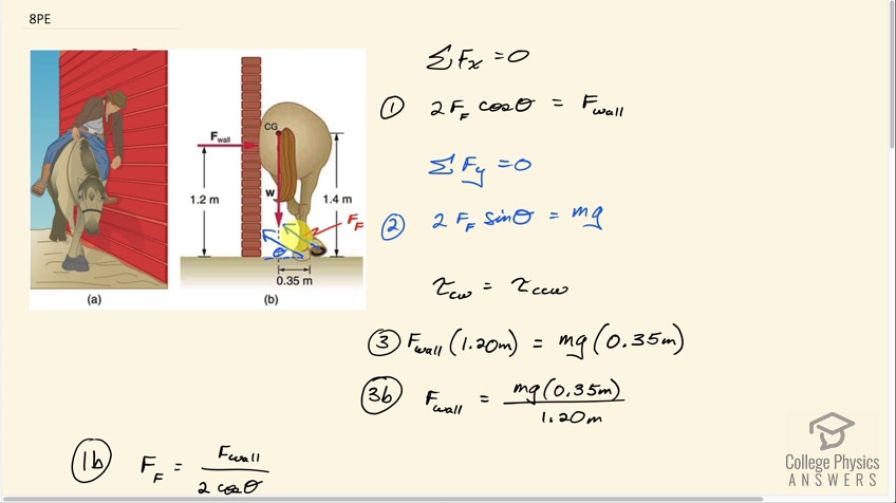
This is College Physics Answers with Shaun Dychko. We are going to calculate the force on each of the feet of this horse and it's going to be a force that is somewhat upwards to balance the weight of the horse and rider and it's also going to be somewhat to the left to balance the force exerted by the wall to the right and so it's gonna have some angle Θ here above horizontal towards the wall. So the first condition of equilibrium is to say that the total forces in the x-direction and in the y-direction equal zero or you could say that the forces to the left equal the forces to the right. So this is 2 times because there are two feet 2 times the force on a single foot multiplied by cosine Θ to give us this component which is horizontal here that equals the force exerted by the wall to the right. And then we can talk about the y-direction and say that the vertical component of the force exerted by a foot multiplied by 2 equals the total weight downwards, mg. And there are three unknowns here: we don't know the force exerted by the wall nor Θ nor do we know the force on a single foot and so we need to have three equations to solve three unknowns and so far we have two equations and then we'll use the second condition of equilibrium which says that the total clockwise torque has to balance the total counter clockwise torque to find equation (3). So we have the force exerted by the wall multiplied by its perpendicular distance to the pivot at the foot—1.20 meters— equals the counter-clockwise torque due to the weight which is 0.35 meters perpendicular distance to the pivot. So we divide both sides by 1.20 meters here and this gives us the force exerted by the wall mg times 0.35 divided by 1.20 and then we can do some substituting and rearranging to eventually solve for some of the unknowns. So returning back to equation (1), we can solve it for the force exerted on a foot and it's going to be the force exerted by the wall divided by 2cos Θ when you divide both sides by 2cos Θ here and then substitute in the force exerted by the wall in place of F wall here. So this is substituting equation 3 version b in place of equation [1b] and then we'll call this result equation [1c] so we have mg times 0.35 meters divided by 2cos Θ times 1.20 meters. Then we'll look at equation 2 version b and substitute in what we have for the force on a foot equation [1c] in place of F in equation 2 version b. So solving... rewriting equation 2 but instead of the force on a foot, we are gonna write mg times 0.35 meters divided by 2cos Θ times 1.20 meters and so we do that here. Now whole bunch of things cancel which is convenient: the mg's cancel, these 2's cancel and sin Θ divided by cos Θ can be replaced with tangent Θ— that's a trigonometric identity— and that's gonna equal 1.20 meters divided by 0.35 because the other thing we'll do here is multiply both sides by 1.20 and divide both sides by 0.35 and Θ then is gonna be inverse tangent of 1.20 divided by 0.35 which is 73.7 degrees. Then returning back to equation 2, we'll call it version c, where we solve for the force on a foot that's going to be mg divided by 2sin Θ. We have 500 kilograms—total mass of the horse and rider— times 9.8 newtons per kilogram divided by 2 times sin of this angle that we just found and that is 2550 newtons. So the force on a single foot is 2550 newtons, 73.77 degrees above horizontal towards the wall. Then the next question in part (b) asks what is the minimum coefficient of static friction that's necessary to keep these feet from slipping. So the total friction force is 2 times the horizontal component of a force on a foot and that also is going to be the coefficient of static friction multiplied by the normal force which will in turn equal the weight of the horse and rider. So we'll solve for μ s by dividing both sides by mg so that's 2 times the force on a foot times cos Θ divided by mg. So that's 2 times 2552.1 newtons times cos of 73.7398 degrees divided by 500 kilograms times 9.8 newtons per kilogram which is 0.292 and that is the minimum coefficient of static friction.