Question
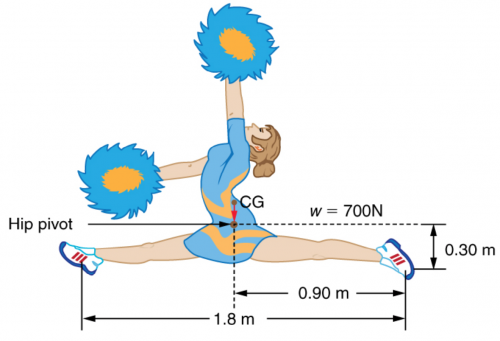
A gymnast is attempting to perform splits. From the information given in Figure 9.35, calculate the magnitude and direction of the force exerted on each foot by the floor.
Final Answer
above horizontal toward the center of gravity.
Solution video
OpenStax College Physics for AP® Courses, Chapter 9, Problem 16 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
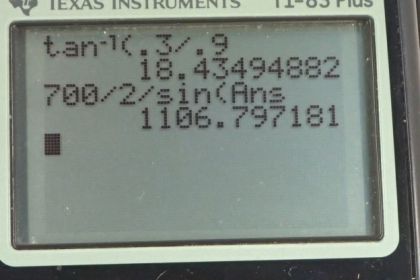
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to calculate the force on each foot of this gymnast who's doing the splits. We have to make some assumptions because there isn't really enough information given to properly answer the question; it wasn't clear to me whether the force on the foot was straight up or whether it should be along the legs but since it is asking for the direction of the force, we are gonna assume that they must be expecting some answer that's more complicated than just straight up. So we are gonna have the force going along the leg so it's at this angle Θ which we can calculate because we know that tangent Θ will be opposite this height to the center of gravity divided by this adjacent which is the length of the leg horizontally. So that's 0.30 divided by 0.90 is tan of Θ and which means that Θ is the inverse tan of that which is 18.4 degrees. So we know that the vertical components of these two forces have to balance the gravity downwards. So 2 times F times sin Θ— which gives the opposite leg of this force here— has to equal the weight downwards and we can rearrange this for F by dividing both sides by 2sin Θ and we have that F is the weight divided by 2sin Θ. So that's 700 newtons divided by 2 times sin of 18.435 degrees giving us an answer of 1.11 times 10 to the 3 newtons, 18.4 degrees above horizontal towards the center of gravity.