Question
When you use your hand to raise a 20 lb dumbbell in a curling motion, the force on your bicep muscle is not equal to 20 lb.
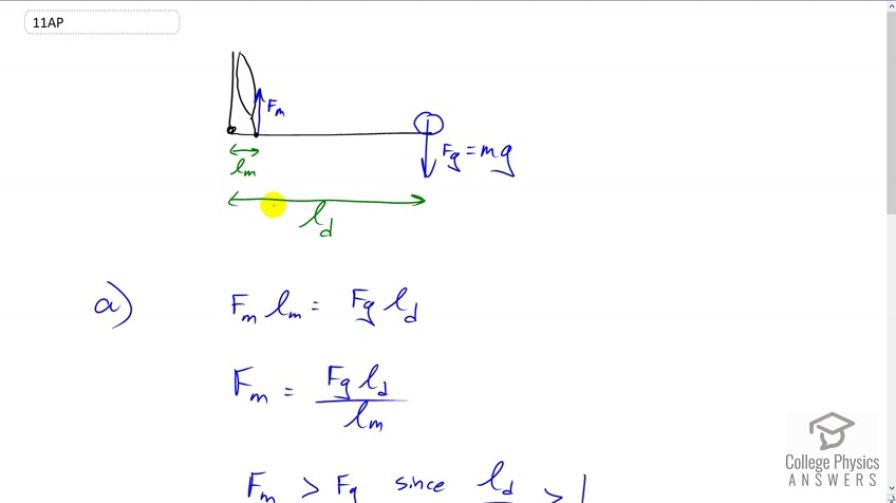
- Compare the size of the force placed on your bicep muscle to the force of the 20 lb dumbbell lifted by your hand. Using the concept of torque, which force is greater and explain why the two forces are not identical.
- Does the force placed on your bicep muscle change as you curl the weight closer toward your body? (In other words, is the force on your muscle different when your forearm is 90° to your upper arm than when it is 45° to your upper arm?) Explain your answer using torque.
Final Answer
a) The bicep muscle exerts more force than the weight of the dumbell.
b) The bicep muscle probably exerts less force. See the solution video for discussion.
Solution video
OpenStax College Physics for AP® Courses, Chapter 9, Problem 11 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. When holding a twenty pound dumb-bell in the hand, that dumb-bell will exert a torque equal to its weight multiplied by its distance from the elbow, call that lever arm d for dumb-bell. Then a torque in the opposite direction will be exerted by the bicep muscle and so there'd be a force upwards wherever this tendon attaches to the arm and that'll be some distance from the elbow, call it l subscript m for muscle. So the force of the muscle times the lever arm of the muscle must equal the force of gravity on the dumb-bell, multiplied by the lever arm of the dumb-bell. We can divide both sides by l m to solve for the force on the muscle. We can see that the force exerted by the muscle has to be much greater than the weight of the dumb-bell since the lever arm of the dumb-bell is greater than the lever arm of the muscle. So l d over l m is going to be greater than one. So we're going to be multiplying the weight of the dumb-bell by some number more than one. So that's going to make the force exerted by the muscle greater than the weight of the dumb-bell. Then when the bicep is curled, so that you know, you have this angle maybe 45 degrees say, what change will there be? In this case, will the force exerted by the muscle change? Now, bio-mechanics is a little bit complicated and the body is not a machine that we can draw perfect pictures for. So there are two possible answers to this question. One is that there is no difference, and two is that there is a less force exerted by the biceps. So I've taken the route here where I'm going to conclude that there is less force. But I'll tell you why you could say that there is equal force in a second. So, let's assume that when the bicep is curled, the bio-mechanics are such that this force exerted by the muscle is still perpendicular to the arm, in which case the lever arm for the muscle is going to be the same as it was in part A. So we'll say that the perpendicular component of the lever arm for the muscle is this distance along the arm which is l m just as it was in part A. When that's the case, well, the dumb-bell is losing some of its lever arm and so its torque is going to be reduced and with the lever arm of the muscle staying the same, it'll mean that the muscle force will reduce. So in this case here, we have lever arm of the dumb-bell two, so the second case, is going to be the lever arm in the first case, part A, multiplied by sine theta. That gives us this component here, this opposite leg of this triangle and we're multiplying it by l d which is the lever arm that it had in part A which goes from here along the arm to here, length of the arm in other words, and we substitute that in for the lever arm of the dumb-bell, and we're dividing by l m, just as we did before. This is going to be less than the expression we had for the force in the muscle in part A because sine theta is always less than one when theta is between zero and 90. So we can conclude that the force of the muscle in the second case will be less than the force of the muscle in the part A. Now, maybe you can make different assumptions about the bio-mechanics here in which case the -- perhaps the lever arm of the muscle has changed in the same way that the lever arm of the dumb-bell has. Although I don't think it has. I mean, experience says that when you curl the dumb-bell it gets easier to hold it when it's closer to your body. So I think this picture is the more accurate one. But what if the muscle was still exerting a force upwards and the lever arm of it was changing in the same way as it is for the dumb-bell, then you would say l m, the lever arm for the muscle would be l m times sine theta as well, in which case the sine theta's would cancel and you'd have the same answer as before. But I think experience shows that this picture with the muscle exerting a force perpendicular to the arm and the lever arm is not changing when it's curled, is the more realistic picture.