Question
What force does the nail puller in Exercise 9.19 exert on the supporting surface? The nail puller has a mass of 2.10 kg.
Exercise 9.19
What is the mechanical advantage of a nail puller—similar to the one shown in Figure 9.24 —where you exert a force 45 cm from the pivot and the nail is 1.8 cm on the other side? What minimum force must you exert to apply a force of 1250 N to the nail?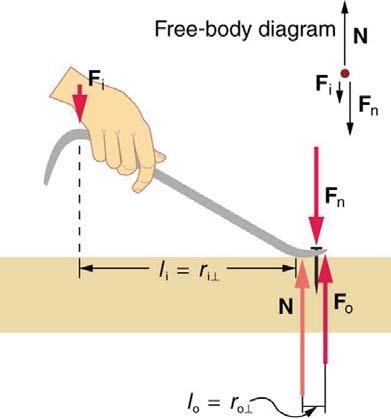
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 9, Problem 23 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This question asks us to find this normal force exerted by the ground on the nail puller here at the pivot. There are going to be three forces that are down, one is the input force, the other is the weight of the nail puller, and then the third force is this reaction force exerted by the nail head on the end of the nail puller. That reaction of course is going to equal the output force exerted upwards on the nail by the nail puller. So we know that the input level arm is 45 centimeters and the output level arm is 1.8 centimeters, that’s what question 19 tells us. We can find the input force by dividing the output force times its level arm by the input level arm in equilibrium just at that moment when things are about to start moving, we have the input torque equals the output torque. We can divide both sides by li to solve for Fi. The normal force exerted upwards by the ground on this pivot point equals the three forces that are down, totaled together. The Fn, being the Newton’s third law counterpart to Fo, they are of equal magnitude, so I can substitute Fo in place of Fn. Also I’ve made a substitution mg for the force of gravity on the nail puller, and then we make a substitution Fo lo over li in place of the input force. We can factor out the Fo, it’s l naught over li plus one, and we have 1250 newtons is needed to pull out the nail, that’s the output force, multiplied by the output level arm of 1.8 centimeters divided by the input level arm of 45 centimeters plus one, plus 2.1 kilograms times 9.81 newtons per kilogram, and this gives us 1.32 times ten to the three newtons is the normal force applied upwards on the pivot by the surface.
