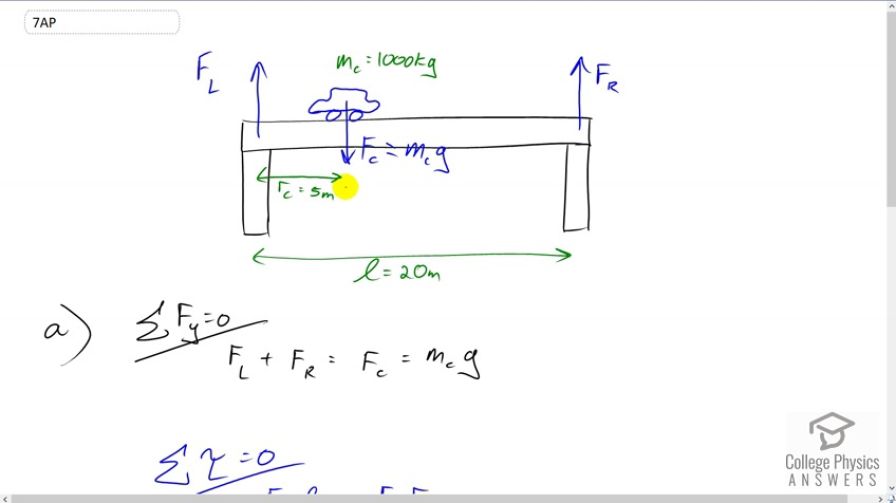
Question
A bridge is supported by two piers located 20 meters apart. Both the left and right piers provide an upward force on the bridge, labeled FL and FR respectively.
- If a 1000 kg car comes to rest at a point 5 meters from the left pier, how much force will the bridge provide to the left and right piers?
- How will FL and FR change as the car drives to the right side of the bridge?
Final Answer
a) ,
b) As the car crosses the bridge the force on the left pier will decrease while the force on the right pier will increase.
Solution video
OpenStax College Physics for AP® Courses, Chapter 9, Problem 7 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have two piers that are twenty meters apart supporting a bridge and there is a one thousand kilogram car positioned five meters from the left pier. We have to figure out what are the forces on each of the piers. Here's the force on the left side, and here's the force on the right side. Now it says what is the force on the pier? But the force on the pier is the Newton's Third Law counterpart to the force that the pier exerts on the bridge. So it's the force on the bridge that we're going to be including in our calculations but it's of equal magnitude to the force that's on the pier. So, forces in the y direction have to equal zero. There are two up forces, the left pier and the right pier force and that has to equal the force on the car going downwards which is mass of the car times g. Then for this second condition for equilibrium is that the total torques have to equal zero. We'll take the pivot to be at the left pier and so we have the counter-clockwise torque due to the right pier, which is the force exerted by the right pier on the bridge, multiplied by its lever arm at twenty meters. That has to equal the torque due to the force on the car multiplied by its five meter lever arm. We can divide both sides by l here to get the force on the right side of the bridge. That's going to be mass of the car times g times the car's lever arm, divided by the pier's lever arm. That's one thousand kilograms times 9.81 newtons per kilogram times five meters lever arm for the car, divided by twenty meters lever arm for the right pier. This gives 2500 newtons. Then the force on the left pier, we can rearrange this formula and subtract F r from both sides and we get that it's m g minus the force on the right pier. So that's one thousand kilograms times 9.81 minus 2452.5 and we get about 7400 newtons is the force on the left pier. We can see that the left pier is exerting a lot more force than the right one. That's not surprising because the car is closer to the left one than it is to the right one. As the car moves to the right on the bridge, the force on the left pier will decrease while the force on the right pier will increase. I mean once this car gets to a position that's five meters from the right pier then these numbers should switch places and then the left pier will be exerting 2500 newtons when the right pier will be exerting 7400.
