Question
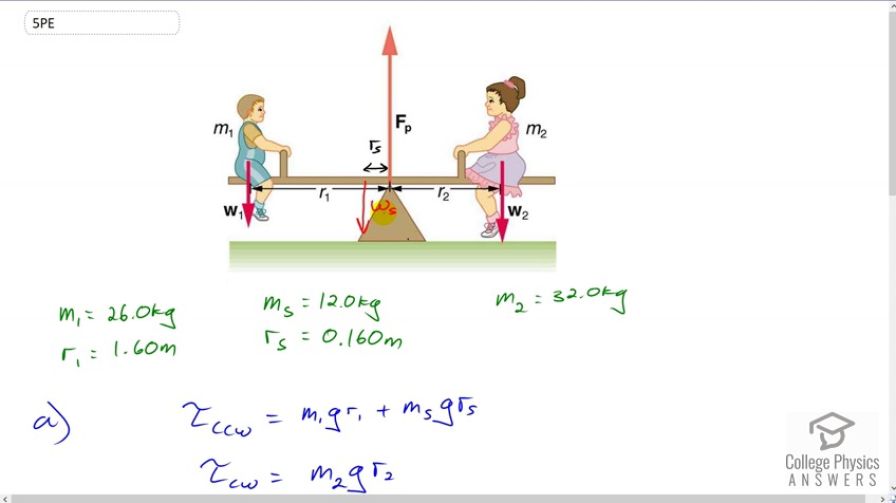
Repeat the seesaw problem in Example 9.1 with the center of mass of the seesaw 0.160 m to the left of the pivot (on the side of the lighter child) and assuming a mass of 12.0 kg for the seesaw. The other data given in the example remain unchanged. Explicitly show how you follow the steps in the Problem-Solving Strategy for static equilibrium.

Example 9.1

The two children shown in Figure 9.10 are balanced on a seesaw of negligible mass. (This assumption is made to keep the example simple—more involved examples will follow.) The first child has a mass of 26.0 kg and sits 1.60 m from the pivot.(a) If the second child has a mass of 32.0 kg, how far is she from the pivot? (b) What is FpF_p, the supporting force exerted by the pivot?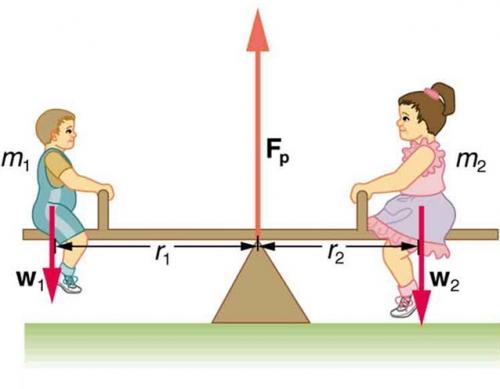
<b>Figure 9.10</b> Two children balancing a seesaw satisfy both conditions for equilibrium. The lighter child sits farther from the pivot to create a torque equal in magnitude to that of the heavier child.
Figure 9.10 Two children balancing a seesaw satisfy both conditions for equilibrium. The lighter child sits farther from the pivot to create a torque equal in magnitude to that of the heavier child.
Question by OpenStax is licensed under CC BY 4.0
Final Answer

a) 1.36 m1.36 \textrm{ m}

b) 686 N686 \textrm{ N}

Solution video

OpenStax College Physics for AP® Courses, Chapter 9, Problem 5 (Problems & Exercises)

OpenStax College Physics, Chapter 9, Problem 5 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Select problem
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 9, Problem 5 (PE) calculator screenshot 1
Video Transcript
This is College Physics Answers with Shaun Dychko. This is the same picture as we have in example 9.1, with the addition of a new weight here due to the seesaw. So it’s w subscript s for seesaw, and it’s positioned at some distance from the pivot r subscript s, so this is the center of mass of the seesaw. And it’s going to exert a counter-clockwise torque in the same direction as the torque exerted by this boy. We know that for static equilibrium to occur, we have the total counter-clockwise torque has to equal the clockwise torque. And so we create expressions here for each. So we have the weight of the boy multiplied by his distance from the pivot and then add to that the torque due to the seesaw, and that’s going to equal the clockwise torque due to the girl which is m2 times g times her distance from the pivot r2. And we equate these two, and then we solve for r2 and we also divide both sides by g and it will cancel everywhere. So we have the distance that the girl needs to sit from the pivot is going to be m1 r1 plus ms rs, all divided by m2. So it’s 26 kilograms mass of the boy times 1.6 meters, plus 12 kilograms mass of the seesaw times 0.16 meters, divided by 32 kilograms mass of the girl, and that gives a position of 1.36 meters from the pivot. The next question is what should this force due to the pivot be, and by the way, this force did not appear in our torque calculation because the level arm for this force is zero because it’s positioned at the pivot. And so it doesn’t exert any torque above the pivot, but it does exert a force obviously, that’s what supporting this whole seesaw and the kids. And so the total force upwards, which is consisting only of this one force due to the pivot, has to equal the total force down, which is the weight of the boy and the girl and the seesaw. We can factor out the g there, common factor. So we have the force of the pivot is g times the total mass, so that’s 9.8 newtons per kilogram gravitational field strength, multiplied by 26 kilograms mass of the oy plus 32 kilograms mass of the girl plus 12 kilograms mass of the seesaw, giving 686 newtons.