Question
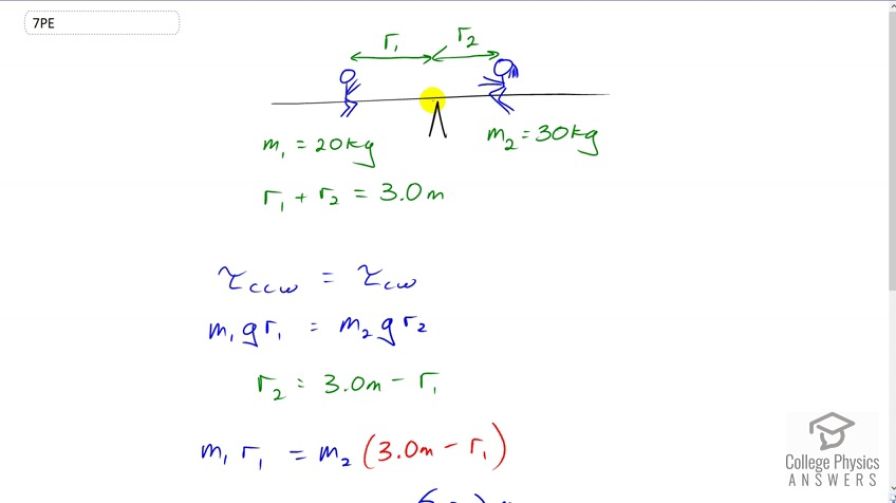
Two children of mass 20 kg and 30 kg sit balanced on a seesaw with the pivot point located at the center of the seesaw. If the children are separated by a distance of 3 m, at what distance from the pivot point is the small child sitting in order to maintain the balance?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 9, Problem 7 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We know that a boy of mass 20 kilograms is sitting on one side of the pivot on the seesaw and a girl of mass 30 kilograms is sitting on the other side and they are meant to be in static equilibrium. So that means that they are exerting the same magnitude torques in opposite directions and the total distance between them is three meters. So that means the level arm of boy one which is r1 plus the level arm of the girl which is r2 has to equal three. So, we’ll use that in a second. First of all, let’s just say that the counter-clockwise torque has to equal the clockwise torque. And so the counter-clockwise torque is due to the boy, so that’s its weight multiplied by its level arm, so that’s m1 g times r1 and then for the girl, it’s m2 g times r2. The weight is perpendicular to the level arm already so we don’t need to be concerned with angles here, or you could just go sine of 90 degrees which should be the number one. So then we use this fact here to replace the r2 in this equation in order to have an equation consisting of only one variable r1 which we’ll then solve for. So we replace r2 with three meters minus r1, and then we solve for r1. So we multiply through by m2, then we get m2 times r1 here with a minus in front of it and then we add that to both sides, then we get this line here. We have m1 r1 plus m2 r2 equals three m2. And then factor out the r1, which is a common factor among these two terms, and then divide by the bracket m1 plus m2 that we get, and then you end up with r1 is three times m2 divided by m1 plus m2. So that’s three meters times 30 kilograms divided by 20 kilograms plus 30 kilograms, which is 1.8 meters is the distance from the pivot that the boy needs to sit in order to create a torque that balances the torque exerted by the girl in the opposite direction.
