Question
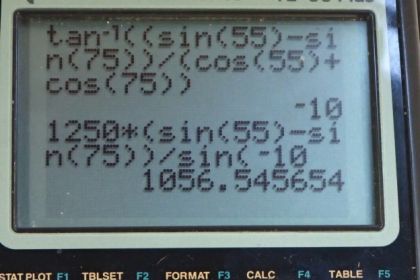
The upper leg muscle (quadriceps) exerts a force of 1250 N, which is carried by a tendon over the kneecap (the patella) at the angles shown in Figure 9.37. Find the direction and magnitude of the force exerted by the kneecap on the upper leg bone (the femur).
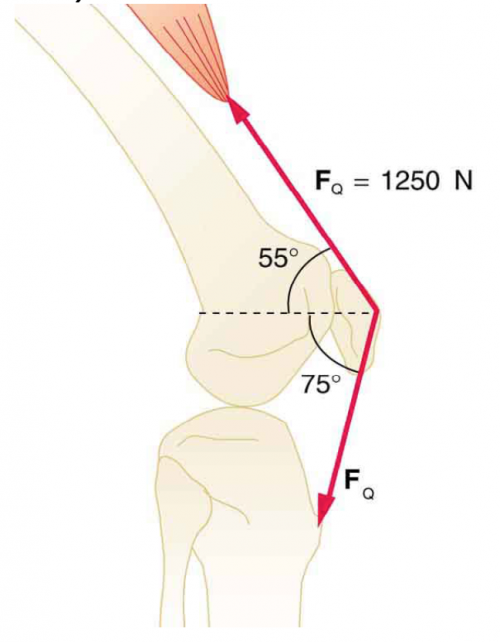
Final Answer
below horizontal to the left.
Solution video
OpenStax College Physics for AP® Courses, Chapter 9, Problem 28 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to calculate the force on the femur due to the patella, which is the name for the kneecap, but in this picture, I'm drawing the force on this tendon which is exerted we assume in this direction so this is force due to the kneecap on the tendon at some angle Θ below horizontal. So these three forces have to balance: this is the force due to the quadricep which is a tension that's the same in this segment of the tendon as well as this segment of the tendon but these angles are different— 75 degrees versus 55. Now the vertical forces have to add up to zero so we can take the upwards component of this force F Q—for quadricep—times sin 55 because that's the opposite leg of this triangle here and that upwards force has to equal the total downward forces so that's F Q times sin 75 plus this F K—that we don't know— multiplied by sin of Θ—that we also don't know. So because there are two unknowns, we need to have a second equation to solve for them so let's consider the total horizontal forces adding up to zero or the forces to the right have to equal the total forces to the left. So F K multiplied by cosine Θ gives us this horizontal component here due to the force due to the knee and that equals F Q times cos 55 plus F Q times cos 75. Now we can rearrange this formula here for F K by subtracting F Q sin 75 from both sides and then dividing both sides by sin Θ and then divide this by sin Θ and you end up with this line here and that's useful because we can then replace F K in this blue formula with all of this and then we have only one unknown which is Θ. So I have rewritten the horizontal... you know, condition for equilibrium but I have replaced the F K with this expression here. Now we have cos Θ divided by sin Θ but we would prefer is to have sin Θ divided by cos Θ because that's replaceable by the trigonometric identity tangent Θ. So I am multiplying both sides by sin Θ over cos Θ so that makes sin Θ over cos Θ on this side and over here all the trig terms cancel and then we are also dividing both sides by F Q so that cancels and then we are dividing both sides by this bracket cos 55 plus cos 75 and that leaves us with this line here once we have switched the sides around. So we have sin Θ over cos Θ is sin 55 minus sin 75 divided by cos 55 plus cos 75 and all of this is tan Θ. So that means Θ then is the inverse tan of this expression here and that works out to negative 10 degrees. Now the significance of the negative sign is that we have made a wrong assumption about the direction so the negative sign means Θ is measured in the opposite way that we have drawn it and so in fact, F K is this direction like this with Θ being 10 degrees above horizontal. But anyway, we can still work with this angle and plug it into our formula for F K so now we place Θ with negative 10 now. So we have 1250 newtons force due to the quadricep times sin 55 minus sin 75 divided by sin of negative 10 which is 1060 newtons. So this is the force on the tendon due to the kneecap 1060 newtons, 10 degrees above horizontal to the right and it's the force that's on the femur though that we are concerned with and that's the Newton's third law counterpart so opposite direction then but the same magnitude. So the force on or due to the patella— P for patella— is 1060 newtons, 10 degrees below horizontal to the left.