Question
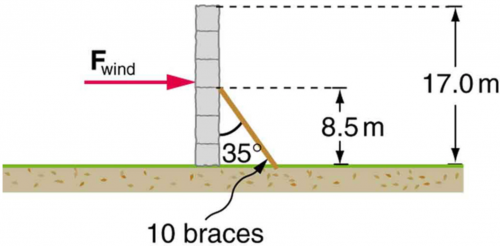
A 17.0-m-high and 11.0-m-long wall under construction and its bracing are shown in Figure 9.31. The wall is in stable equilibrium without the bracing but can pivot at its base. Calculate the force exerted by each of the 10 braces if a strong wind exerts a horizontal force of 650 N on each square meter of the wall. Assume that the net force from the wind acts at a height halfway up the wall and that all braces exert equal forces parallel to their lengths. Neglect the thickness of the wall.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 9, Problem 10 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
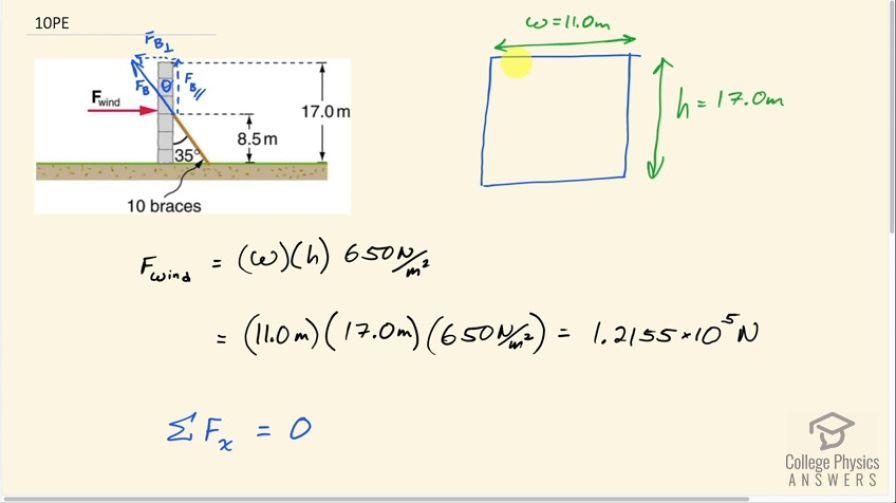
This is College Physics Answers with Shaun Dychko. There's wind blowing on this wall and exerting a force of 650 newtons for every square mater of wall surface area so we need to calculate the area of this wall. We are told that it's 11.0 meters long and 17.0 meters high and so we'll take that area of the length times the height I call the 'w' for width but anyway... you get the idea. So this dimension multiplied by the height multiplied by 650 is the total force exerted by the wind on the wall. So that's 11.0 meters times 17.0 meters times 650 which is 1.2155 times 10 to the 5 newtons. We assume that this force is exerted in the middle of the wall so 8.50 meters above the ground but we are not actually going to use that fact for anything here we are going to use the first condition of equilibrium which is to say that the total horizontal forces have to add up to zero or you could say the total force to the left has to equal the total force to the right and this here is the total force of all ten braces together perpendicular component. So this force is along the brace, we are told, and we can find a component perpendicular to the wall and the component parallel to the wall; it's the perpendicular one that we are interested in because that's the one that has to balance the force exerted by the wind so F B perpendicular equals force of the wind. And this is the opposite leg of this triangle and so we need to use sin Θ multiplied by the hypotenuse to find F B perpendicular. So we have F B sin Θ equals force exerted by the wind and divide both sides by sin Θ and we solve for the total force of all ten braces. So that's 1.2155 times 10 to the 5 newtons divided by sin of 35 degrees because this Θ is opposite to this angle here and so these opposite angles are equal and that's 2.12 times 10 to the 5 newtons. Now the force exerted by a single brace is going to be that total force divided by the 10 braces and so 2.12 times to the 4 newtons is the force exerted by a single brace.
