Question
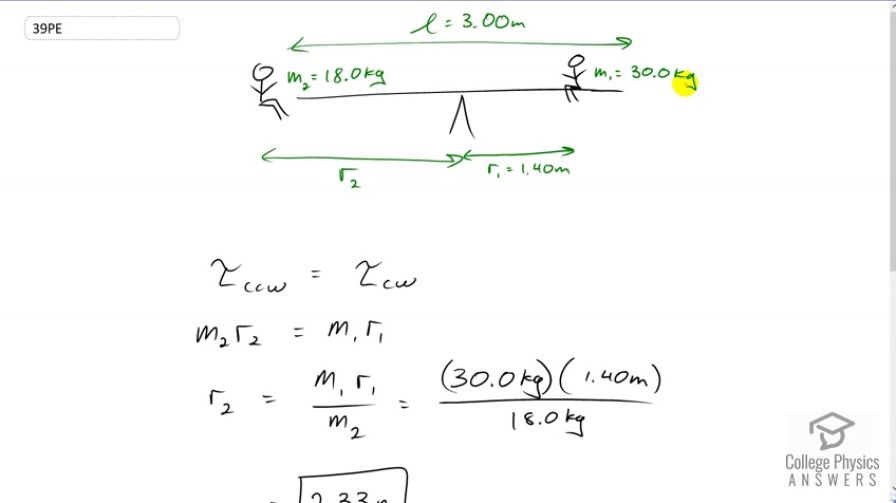
Suppose two children are using a uniform seesaw that is 3.00 m long and has its center of mass over the pivot. The first child has a mass of 30.0 kg and sits 1.40 m from the pivot. (a) Calculate where the second 18.0 kg child must sit to balance the seesaw. (b) What is unreasonable about the result? (c) Which premise is unreasonable, or which premises are inconsistent?
Final Answer
a)
b) Child two is past the end of the seesaw!
c) The first child must be moved closer to the pivot.
Solution video
OpenStax College Physics for AP® Courses, Chapter 9, Problem 39 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A seesaw is 3 meters long and child one is positioned at 1.4 meters from the pivot and he has a mass of 30 kilograms. Child two has a mass of 18 kilograms. So the question is where should child two be positioned so that the seesaw is balanced. Well, the counter-clockwise torque has to equal the clockwise torque so child two's mass multiplied by the lever arm -- well technically I suppose we should be saying mass times gravitational field strength g to get the weight. But the g's are going to cancel on both sides, so let's cancel those. Then divide both sides also by m two and we'll solve for r two. So that's 30 kilograms times 1.4 meters divided by 18 kilograms and that gives 2.33 meters. But there is a problem with that because child two is past the end of the seesaw. We're told that the pivot is in the center and so the seesaw sticks out only 1.5 meters on either side and this child two has to be at a position of 2.3 meters. So that's unreasonable, and probably the first child should just move closer to the pivot in which case they'll have less torque, r one will be reduced, to the point where r two will finally fit on this end of the seesaw.
