Question
Suppose identical amounts of heat transfer into different masses of copper and water, causing identical changes in temperature. What is the ratio of the mass of copper to water?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 14, Problem 7 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
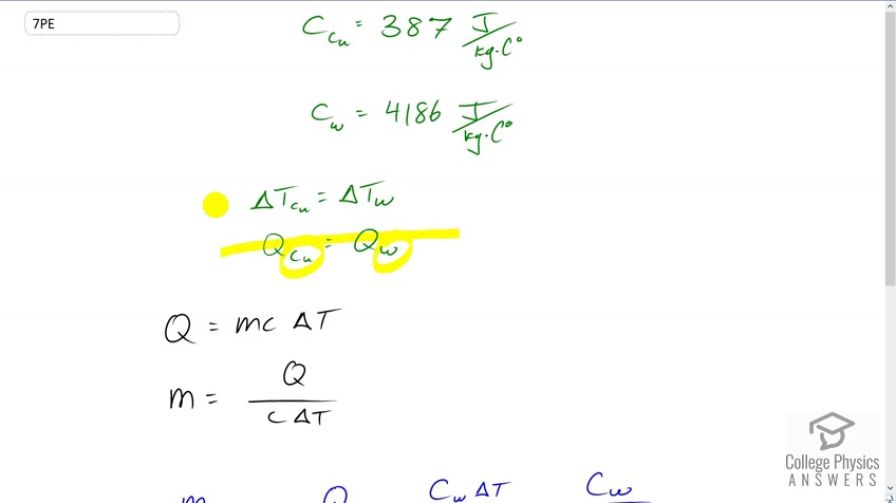
This is College Physics Answers with Shaun Dychko. Identical amounts of heat are transferred into a sample of copper and a sample of water. That results in the same change in temperature for the two samples. We need to use this information to figure out what the ratio of the masses must be. And the specific heat of copper is 387 Joules per kilogram per Celsius degree. The specific heat of water is 4186 Joules per kilogram per Celsius degree. So, the heat transferred into a substance is equal to its mass times its specific heat times its change in temperature and we'll solve this for M because we're going to divide the mass of the copper by the mass of the water because that'll be the ratio of the masses. And so, we're going to find expressions for mass in terms of heat, specific heat, and temperature. So, we'll divide both sides by C Delta T. And then, we get mass, after we switch the sides around, equals Q over C Delta T. So, the mass of copper divided by the mass of water is this expression for copper, Q over C subscript Cu to say this is the specific heat of copper, times Delta T. And, notice the Q and the Delta T do not have subscripts of Copper because these variables are the same for both samples, the copper and the water, have the same Q and the same Delta T, and so there's no need for a subscript to distinguish them. And then, we're going to divide by the same expression but for water and dividing a fraction by a fraction is messy, so instead I'm going to multiply by the reciprocal of the denominator's fraction. So, we're going to multiply by the reciprocal of this for water. So, multiplying by Cw, specific heat of water, times Delta T over Q. The Q's and Delta T's cancel, leaving us with the specific heat of water divided by the specific heat of copper. So, the mass of copper to the mass of water, the ratio, is 4186 Joules per kilogram per Celsius degree, divided by 387, and that gives 10.8. So, there's 10.8 times as much copper as there is water. So, if you wanted to solve the mass of copper, 10.8 multiplied by mass of water. So, there's more copper, in other words.
