Question
The rate of heat conduction out of a window on a winter day is rapid enough to chill the air next to it. To see just how rapidly the windows transfer heat by conduction, calculate the rate of conduction in watts through a window that is 0.635 cm thick (1/4 in) if the temperatures of the inner
and outer surfaces are and , respectively. This rapid rate will not be maintained—the inner surface will
cool, and even result in frost formation.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 14, Problem 31 (Problems & Exercises)
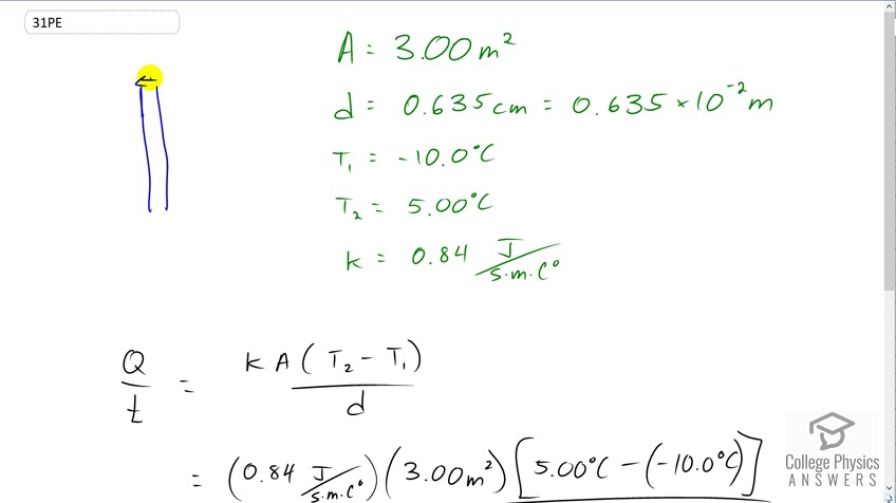
vote with a rating of
votes with an average rating of
.
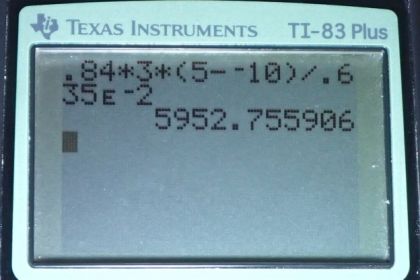
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a window pane which is made up of glass and the glass is a quarter inch thick which is 0.635 cm thick which we write in meters as 0.635 times 10 to the minus 2 meters. The area of this window pane if you were to look at it face on is 3 meter squared and we have the inside of the house here, here's the floor and this temperature inside which is T2. Because this formula for the rate of heat conduction is the rate of heat conduction from body 2 towards body 1 and so the heat is going from the inside of the house which is at 5 degrees and its going to the outside which is T1 which is negative 10 degrees Celsius and the thermal conductivity of glass is 0.84 Joules per second per meter squared per Celsius degree squared. OK. So maybe that's not squared there. Yeah, OK. And it’s actually not squared because we have a meter squared here but one of the meter squared in that area gets canceled by this thickness so leaving only 1 meter to the power of 1 in this denominator. OK. So let’s, well, we have written down our formula for the rate of heat conduction and this is the thermal conductivity of the material times with area divided by its thickness and we just plug in numbers. So it’s 0.84 Joules per second per meter per Celsius degree and then times up by 3 square meters area of the window times temperature inside 5 degree Celsius minus the temperature outside which is negative 10 and pay attention to the minus negative 10 which makes a plus in the end and divided by the thickness of the window and you end up with six point O times 10 to the 3 watts is the rate of heat conduction through the window pane.