Question
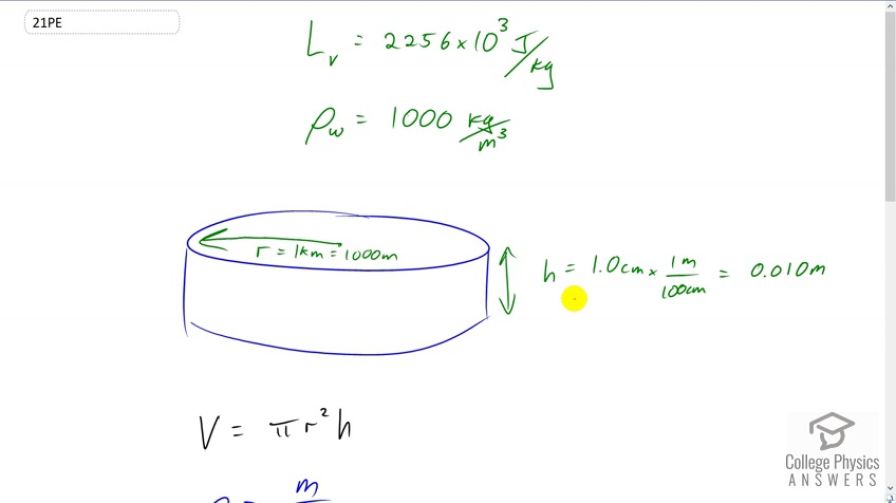
The energy released from condensation in thunderstorms can be very large. Calculate the energy released into the atmosphere for a small storm of radius 1 km, assuming that 1.0 cm of rain is precipitated uniformly over this area.
Final Answer
This amount of energy is comparable to that release during the explosion of a small atomic bomb. The reason the energy from this storm will not create damage in the way the energy from the atomic bomb would is that energy in the two scenarios are released over very different time periods. The power, in other words, is very different. The atomic bomb releases the energy almost instantly, and it's this enormous power that creates damage.
Solution video
OpenStax College Physics for AP® Courses, Chapter 14, Problem 21 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
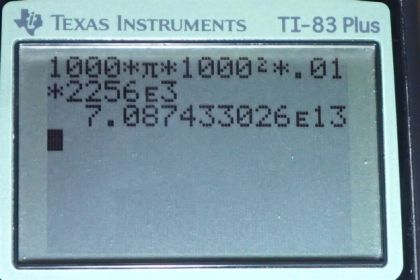
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko A storm, which we’ll assume has a circular shape of radius one kilometer, which his 1000 meters, has precipitated one centimeter of water, which is .01 meters, when you multiply by 1 meter per hundred centimeters. And all of this water in this volume, which is liquid state, must have originated as a vapor. And so, in other words, the vapor condensed to form the water that accumulated here. And so when it did that, it released some heat of vaporization. Or heat of condensation, you might say. So, we need to figure out how much that heat is, and we need to know what the mass of this water is. And we can calculate the volume, and then, knowing that density is mass divided by volume we can solve for mass by multiplying both sides by v, and then switching the sides around, then you have mass is density times volume. And the volume of the cylinder, is the area of one of the round ends multiplied by the height. So that’s, pi r squared, pi times radius squared, multiplied by height. And that’s what I put in here, in place of volume. And the density of water is a thousand kilograms per cubic meter. And the latent heat of vaporization 2256 times 10 to the three Joules per kilogram. So, all of this mass gets plugged into this heat of vaporization formula, which is mass times latent heat of vaporization. It should have a v in there instead of an f. Coz it’s not freezing, it’s turning into liquid. Okay, so we have 1000 kilograms per cubic meter density, times pi, times the radius, 1000 meters squared, times the height of one centimeter, which is .01 meters. Then we multiply that by the latent heat of vaporization to get 7.1 times 10 to the 13 Joules must have been released, due to the condensation of the water vapor. Now this is an enormous amount of energy and it’s comparable to a small atomic bomb explosion. And, the reason why this storm does not cause the same destruction as an atomic bomb, is because, even though the energies are comparable, the time during which this energy is released is very different. So an atomic bomb would release all this energy in seconds, whereas a storm will take several hours to release it.