Question
A 0.0500-kg ice cube at is placed in 0.400 kg of water in a very well-insulated container. What is the final temperature?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 14, Problem 24 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
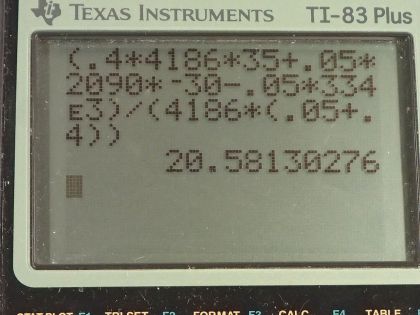
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A 0.0500 kilogram ice cube is put into some water which has a mass of 0.400 kilograms and the ice cube's initially at a temperature of minus 30.0 degrees Celsius and the water is initially at a positive 35.0 degrees Celsius. So some heat is gonna go from the water into the ice cube and melt it and then raise its temperature up to be the same temperature as the water but the water is not gonna have a temperature of 35.0 degrees Celsius anymore since it's losing this heat energy to the ice, its temperature will be dropping and so it's gonna be some temperature, you know, between 0.0 and 35.0 is gonna be the final temperature of the water and that's the question is to figure out what that temperature is? So we start by saying here's an expression for the heat gained by the water and I say gained just to emphasize that this formula is a heat gain and of course the water is losing heat and it ends up being negative because the final temperature will be less than the initial temperature and this will be a negative in this bracket. But down here, we compensate for that by saying that the heat gained by the ice is the opposite of the heat gained by the water or you could say that the heat gained by the ice is whatever is lost by the water and so we want to know what the heat loss is of the water and so to turn this expression Q— which is a gain—into a loss, we put a negative sign in front of it. Another way to think about it is... well, the magnitude of these Q's are gonna be the same and now this one for the water is going to be a negative and so to make it positive, put a negative sign in front of it— it's another way to look at it. So the magnitudes of the heat transfer— two are from water and two are from ice— will be the same because whatever is gained by the ice is lost by the water. So let's talk about the water first; it's gonna have some mass times its specific heat times the change in temperature and we see the final temperature is in this term here and multiplying into this bracket by mass water times specific heat of water. And then we can talk about the ice which is a little bit more complicated; it first has a temperature change from some initial temperature of minus 30.0 up to 0.0 and it will gain an amount of heat equal to its mass times the specific heat of ice times that temperature difference and then it will gain some heat equal to whatever is needed to change its phase from ice into liquid so we have mass of ice times the latent heat of fusion to figure out what that amount of heat is and then furthermore, change the now liquid... you know, what was once ice has now turned into liquid and that same mass... I still have the subscript ice here to indicate it's the mass of what was initially an ice cube but it's in the water state in this term but it's the same mass being multiplied by specific heat of water to some final temperature minus 0.00, which is what this water starts at after the ice has been melted. So this T final and this T final are the same and so they don't have subscripts; there's no w 1 here and there's no ice on here, it's the same final temperature since they are in contact with each other. And this line here I just got rid of anything that was zero so m ice times c ice times 0.00 is just 0.00 so let's just call this minus m ice times c ice times T initial of the ice. And then I took this term over here, m ice c w times T f— that's the first term here— and then plus this heat due to the phase change. Okay! Now the heat gained by the ice again is the heat lost by the water so let's put a negative sign in front of the Q for water and that turns it into a loss and so we are copying this here (use a highlighter) we are copying this down here unchanged and then I said equals the negative of this expression here which is the heat gained by the water. And I hope I am not confusing you when I say the heat gained by the water... I am just trying to be very methodical and you know, sticking to the idea that this expression is for heat gained by something which can be negative in which case you can interpret it as a loss which is the case here. Alright! So distributing this negative sign into the brackets gives us this line here and this line I just copied unchanged and that's what this, you know, horizontal line with two tick marks in it indicates. So we just copy this here and this is positive m w c w T iw minus m w c w T f. Then this term is moved to the left hand side so it becomes— you have to add it to both sides, in other words— and this term goes to the right hand side by adding it to both sides and then this term gets subtracted from both sides. Okay so we have a minus m ice times L f on the right hand side; we have a plus m ice c ice T i ice on the right hand side; and then this term was copied. Okay! So then T f times specific factor of water can be factored out from these terms and then the right hand side is just copied and then at long last, we have an expression for T f by dividing both sides by c w times (m ice plus m w). And so this right hand side... all of it's copied here and is being divided by these factors and then we plug in numbers! So we have 0.400 kilograms of water times 4186 joules per kilogram per Celsius degree— specific heat of water— times 35.0 degrees Celsius—the initial temperature of the water— plus 0.0500 kilograms of ice times the specific heat of ice which is 2090 joules per kilogram per Celsius degree times the ice's initial temperature, which is negative 30.0 degrees Celsius, minus the mass of the ice times the latent heat of fusion—334 times 10 to the 3 joules per kilogram— and we divide all that by the specific heat of water times the total mass of water and ice and that gives 20.6 degrees Celsius is the final temperature of the mixture.