OpenStax College Physics for AP® Courses, Chapter 14, Problem 6 (Test Prep for AP® Courses)

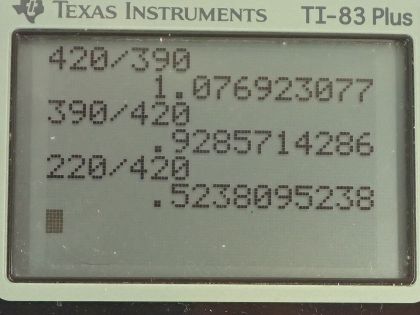
This is College Physics Answers with Shaun Dychko. We are going to design a sauce pan that has the same rate of thermal conduction as a pan made of silver and we are meant to use a less expensive material than silver and the other constraint is that the pan area can be no more than 50 percent greater than the area of the silver pan and then look at what other factors can be adjusted. Okay! So the rate of thermal conduction is the thermal conductivity factor k times the area of that's in contact with the stove element times the difference in temperatures between the stove element and the pan divided by the thickness of the pan. So the rate of thermal conduction for the silver pan will be the thermal conductivity of silver multiplied by the area of the silver pan times this temperature difference divided by the thickness of the silver pan. The temperature difference does not need a subscript for silver because it will be the same temperature difference between whatever material the pan is and the stove. Okay! So the things that can be varied in our attempts at creating a different less expensive pan are the thermal conductivity by choosing a different substance, the area can be adjusted to within one and a half times the area of the silver pan so this one and a half times is 50 percent more and so the area of some whatever substance we don't know what it is yet— we'll call that x— has to be less than or equal to one and a half times the area of the silver pan and we can also adjust this thickness of the pan bottom. Okay! So we look up in table [14.3] for the thermal conductivity of different substances and pans are often made out of things like gold, aluminum and iron and we have steel iron here... it'd be nice to have cast iron but this table doesn't have that but steel iron will be close enough I guess and we don't generally make glass... I guess glass can be used for making a pan and well, not glass wool but this glass here would be the one to use but the thermal conductivity is so low that it would be really a challenge to create a glass pan with the same thermal conductivity. Okay! So thickness can be varied and I put that in a box to say that it's one of our answers because it asks us what other factors can be adjusted so there's the answer to that question— the thickness— and we'll see in what way it can be adjusted in part of our solution later. First we'll consider making a pan out of copper and we'll keep the thickness the same so the thickness of the copper, which has the symbol Cu is the same as the thickness for gold gold symbol by the way... chemical symbol in the Periodic Table of Elements is Ag. Okay! So the thermal conductivity of copper is 390 joules per second per meter per Celsius degree and so we have the rate of thermal conductivity for copper has to equal the rate of thermal conductivity for the silver; keeping the thicknesses the same means that we do not put a subscript Cu or Ag on the thickness because the thicknesses are the same and so there's no need to distinguish them with subscripts and now we'll multiply both sides by d over T 2 minus T 1 and then also divide both sides by the thermal conductivity of copper and then we isolate the area of the copper pan. So it's going to be the thermal conductivity of silver times the area of the silver divided by thermal conductivity of copper. So that's 420 joules per second per meter per Celsius degree divided by 390 and this works out to 1.08 times the area of the silver pan. So the copper pan is nearly identical in size; it's the same thickness and its area will just be 8 percent more than the area of the silver one. Then consider copper with an equal area so now we are going to vary the thickness and so the area factor does not get a subscript anymore so there's no Cu here and there's no Ag on the other side. We are going to solve for the thickness of copper by multiplying both sides by d Cu and then we'll divide both sides by the thermal conductivity of silver and multiply both sides by the thickness of the silver and then over here multiply by thickness of the silver and divide by thermal conductivity of silver. Okay and we are left with this line here after we switch the sides around. So the thickness of the copper is gonna be thermal conductivity of copper divided by thermal conductivity of silver times the thickness of the silver pan. So that's 390 divided by 420 and that is 0.939 times the thickness of the silver pan. Okay! Then suppose we have a pan made out of aluminum so we look up in our table again for aluminum's thermal conductivity and it's 220 and so we have... the two thermal conductivity's have to be equal to each other and we can solve for d Al— thickness of the aluminum— and we'll multiply both sides by d Al and also multiply both sides by thickness of the silver and then we have to get rid of these factors because we want to have d Al by itself on one side here so let's divide both side by k Ag and area of the silver pan. Okay! So on this right side, which becomes the left after we switch the sides around, we have d Al and then we have thermal conductivity of aluminum times the area of the aluminum times the thickness of the silver divided by thermal conductivity of the silver times the area of the silver. So we can plug in 220 for the thermal conductivity for aluminum divide that by 420 and then we are left with 0.524 times the ratio of the areas times the thickness of the silver. Now this is just an intermediate step here, this is not going to be our answer because we want to know in what way should we be adjusting the area of this aluminum pad and seeing as we have such a low number here... a low factor that suggests that we should maximize the area of the aluminum pan because we want to have maximum thickness for the aluminum pan because if it's too thin then... you know, when you have the coils on an electric stove top suppose if the pan is too thin, you will have hotspots wherever the coil is touching the pan so you have hotspots everywhere we have the wires of the element and I suppose in a gas range, you would also have hotspots although the big advantage with the gas range is that the heat is more distributed evenly. So you don't want a thin pan and so let's maximize this area and we can do that to a maximum of 1.5 times the area of the silver so we are gonna replace A Al with 1.5 times A Ag. Okay! And the area of the silver pan cancels and we are left with the product of 1.5 and 0.5238, which is 0.79 times the thickness of the silver pan is going to be the thickness of the aluminum pan. So the thickness has to be less for the aluminum and we expected that because the thermal conductivity of 220 for aluminum is so much less than 420 for silver and so we need to have a compensatingly thinner bottom for the pan in order to increase our rate of thermal conduction. Okay! Now we consider steel iron, which has a thermal conductivity of 80. From our experience with the aluminum pan, with its thermal conductivity so much less than that of silver, we notice that the area of the aluminum pan had to be maximized at 1.5 times the area of the silver pan and so with this thermal conductivity being even lower still, we should similarly maximize the area of the iron pan and Fe is the subscript for iron by the way in the Periodic Table of Elements. So the area for the iron is 1.5 times the area of the silver pan and I am just jumping straight to this formula for the thickness having done all this work already up here and so we have 80 joules per second per meter per Celsius degree— thermal conductivity for iron— divided by 420 for silver times 1.5 and that is 0.29. So the steel iron pan is going to be only 0.29 times as thick as the silver pan.