Question
In certain large geographic regions, the underlying rock is hot. Wells can be drilled and water circulated through the rock for heat transfer for the generation of electricity. (a) Calculate the heat transfer that can be extracted by cooling of granite by . (b) How long will this take if heat is transferred at a rate of 300 MW, assuming no heat transfers back into the 1.00 km of rock by its surroundings?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 14, Problem 72 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
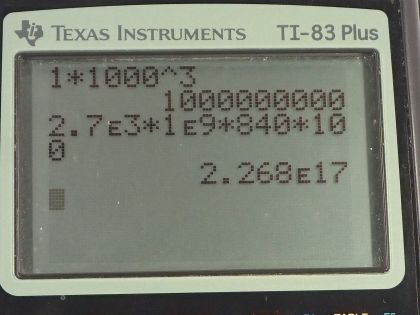
This is College Physics Answers with Shaun Dychko. There's 1.00 cubic kilometer of granite below the surface of the Earth not too far which has some heat in it and the temperature of it is going to be reduced by 100 Celsius degrees in the process of extracting this heat and probably heating buildings or perhaps creating electricity from it. The specific heat of granite is 840 joules per kilogram per Celsius degree and the density of granite is something we need to know and it's 2.7 times 10 to the 3 kilograms per cubic meter— I found this in a data table [11.1] in chapter 11. We convert the cubic kilometers into cubic meters by multiplying by 1000 meters for every kilometer three times and this is 1 billion cubic meters. So the amount of heat extracted from the granite will be its mass times its specific heat times the change in temperature and we can substitute for m by using density. So density is mass divided by volume and we can solve for m by multiplying both sides by V and so m is density times volume and we make a substitution using ρ times V. So the amount of heat that we can extract then is 2.7 times 10 to the 3 kilograms per cubic meter times the volume of 1 billion cubic meters times 840 joules per kilogram times 100 Celsius degrees—temperature change— and that is 2.27 times 10 to the 17 joules. And how long will it take to extract that much energy given a rate of extraction of 300 megawatts; that's part (b). So the power is the amount of energy divided by time and so we'll solve for time by multiplying both sides by t over P. So the time then is the amount of energy divided by the rate at which it is extracted. So that's 2.268 times 10 to the 17 joules divided by 300 times 10 to the 6 watts which is 7.56 times 10 to the 8 seconds which we convert into years by multiplying by 1 hour for every 3600 seconds then by 1 day for every 24 hours and 1 year for every 365.25 days and that's 24.0 years of time for extracting heat from this rock at a rate of 300 megawatts.