Question
Even when shut down after a period of normal use, a large commercial nuclear reactor transfers thermal energy at the rate of 150 MW by the radioactive decay of fission products. This heat transfer causes a rapid increase in temperature if the cooling system fails
(1 watt = 1 joule/second or 1 W = 1 J/s and 1 MW = 1 megawatt)
. (a) Calculate the rate of temperature increase in degrees Celsius per second () if the mass of the reactor core is
kg and it has an average specific heat of
0.3349 kJ/kgo ⋅ C . (b) How long would it take to obtain a temperature increase of , which could cause some metals holding the radioactive materials to melt? (The initial rate of temperature increase would be greater than that calculated here because the heat transfer is concentrated in a smaller mass. Later, however, the temperature increase would slow down because the steel containment vessel would also begin to heat up.)
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 14, Problem 10 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
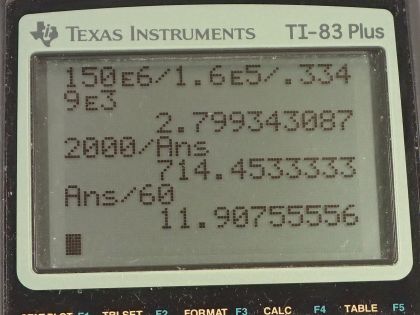
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. When shut down, the nuclear waste from the fission reaction produces heat just by radioactive decay at a rate of 150 megawatts. So this is a power output because it's a rate of energy production. And we'll convert that into watts by multiplying by 10 to the 6. The mass of the nuclear reactor core is 1.60 times 10 to the 5 kilograms and it has a specific heat of about 0.3349 kilojoules per kilogram Celsius degree and we multiply that by 10 to the 3 to turn it into joules per kilogram per Celsius degree. So the amount of heat energy needed to raise a certain temperature is the change in temperature times mass times specific heat and to get the rate of energy... I don't know if heat increase is the right word... heat transfer I should say... the rate of heat transfer is Q divided by t then— that's the power in other words— and that's gonna be mcΔT— change in temperature— divided by the time t. Okay! So we can solve for this change in temperature per time— the rate of temperature increase— by dividing both sides by mc. So we have the rate of change in temperature is power divided by mass times specific heat. So that's 150 times 10 to the 6 watts divided by 1.60 times 10 to the 5 kilograms times the specific heat and that is 2.80 Celsius degrees per second. The time it would take this reactor core to reach 2000 degrees Celsius— at which point, you know, pieces of metal holding the reactor core could melt and then there would be disaster— is 2000 Celsius degrees divided by 2.80 Celsius degrees per second which is 714.45 seconds which is 11.9 minutes.