Question
(a) What is the average useful power output of a person who does of useful work in 8.00 h? (b) Working at this rate, how long will it take this person to lift 2000 kg of bricks 1.50 m to a platform? (Work done to lift his body can be omitted because it is not considered useful output here.)
Final Answer
Solution video
OpenStax College Physics, Chapter 7, Problem 36 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
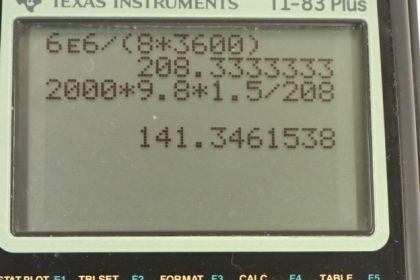
This is College Physics Answers with Shaun Dychko. A person does 6.00 times 10 to the 6 joules of work in 8 hours and so we'll find the power output of this person by dividing that work by the time in seconds. So we multiply 8.00 hours by 3600 seconds per hour, the hours cancel leaving us with seconds on the bottom and we end up with 208 watts. And then in part (b) we are asked given this power output of the person, how long would it take them to lift 2000 kilograms of bricks onto a platform that's 1.5 meters high? So power is useful work done divided by time and we can rearrange this for t by multiplying both sides by t divided by P and we are left with time is work divided by power. So the work done is force times distance or force times displacement multiplied by cosine of the angle between them you could say as well but in this case the force upwards applied by the person is in the same direction as the displacement upwards and so Θ is 0 and cosine of 0 is 1. And then we can replace this F with mg because the force applied we'll assume is just enough to equal gravity downwards so the brick moves at constant speed. So this is the minimum work needed to get the brick onto the platform. So it's mg times the height of the platform, h. We substitute that in place of w and we have time then is mgh divided by power. So that's 2000 kilograms times 9.80 newtons per kilogram times 1.50 meters divided by 208 watts which is 141 seconds.