Question
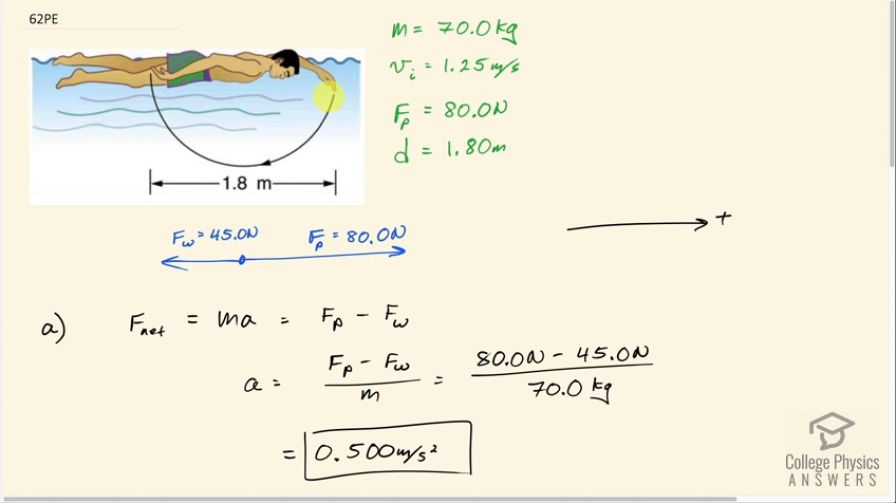
The 70.0-kg swimmer in Figure 7.43 starts a race with an initial velocity of 1.25 m/s and exerts an average force of 80.0 N backward with his arms during each 1.80 m long stroke. (a) What is his initial acceleration if water resistance is 45.0 N? (b) What is the subsequent average resistance force from the water during the 5.00 s it takes him to reach his top velocity of 2.50 m/s? (c) Discuss whether water resistance seems to increase linearly with velocity.
Final Answer
- No, the change in water resistance is not linear with respect to speed. The slope of the resistance vs. velocity graph changes with velocity.
Solution video
OpenStax College Physics, Chapter 7, Problem 62 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This swimmer has a mass of 70.0 kilograms and they are traveling at an initial speed of 1.25 meters per second and the propulsion force that they exert backwards on the water is 80.0 newtons and the water will in turn exert an equal force forwards— that's the Newton's third law counterpart— on the swimmer. And so this is F P for person or propulsion and that is 80.0 newtons forwards on the person and the distance through which their arm moves is 1.80 meters. We are told that the water exerts a resistance force of 45.0 newtons opposing their motion so going to the left then and we'll take right to be positive. Okay! So part (a) asks us what is the initial acceleration given this particular water resistance? So the net force is mass times acceleration and so we can divide by m here to solve for a and we'll divide this by m as well because this is the net force taking all the forces to the right and then subtracting from that all the forces to the left and we end up with this line here. So acceleration is the propulsion force minus the water resistance force divided by the mass that's 80.0 newtons minus 45.0 newtons divided by 70.0 kilograms which is 0.500 meters per second squared. In part (b), we are asked what is the new resistance force in this second period of time during these 5 seconds when he travels from an initial speed of 1.25 meters per second to a final speed of 2.50 meters per second. And to find that force... this, you know, force due to the water in this second case, we need to know what the acceleration is in the second case so I have taken the difference in velocity divided by time. So that's 2.50 meters per second is the final velocity after 5 seconds and subtract from that the initial velocity of 1.25 meters per second and divide it by the time of 5 seconds it takes to change from this speed to that and we get 0.250 meters per second squared and the net force in this second case is gonna be the same propulsion force that doesn't change— the force with which he is pushing back on the water which in turn pushes him forwards— that propulsion force is the same and from that we take the resistance force of the water in the second case and this difference is the net force. So we solve for F w 2 by adding F w 2 to both sides and then also subtract away the net force so that it appears on the right hand side and that's what happens here. So we have F w 2 is F p minus F net 2 and this net force in the second case can be substituted with mass times acceleration in the second case. So we have the force of resistance of the water is 80.0 newtons minus 70.0 kilograms times 0.250 meters per second squared using this acceleration we found there to get a force of 62.5 newtons. In part (c)... and by the way to check whether this is a realistic number we expect some answer that is greater than we had in part (a). So in part (a), the resistance force was 45.0 newtons and drag force is—be it air drag or water drag— they increase with speed and so we expect it with a greater speed, the swimmer to encounter a greater resistance force due to the water so 62.5 newtons is greater than 45.0 so that's good. Part (c) asks us does this resistance force due to the water increase linearly with speed? So for it to increase linearly, we should be able to plot a graph of that resistance force versus the velocity and that graph should be a straight line. And so I have plotted these two things: there's only three points I mean where you can assume that with zero speed, there's zero force and at a speed of 1.25, we have 45 newtons— this lines up with 45 newtons here— and then at 2.5 meters per second, we have a force of 62.5 newtons and we can see from this graph that this is not a straight line graph. I mean it has two segments that each have a different slope and so I have calculated the slope in each case. This letter k is just some letter I made up for representing this constant by which we are supposing we can multiply the velocity by to get the resistance force. And so in the first case, it's 45 newtons divided by 1.25 meters per second— that is this rise here divided by this run— and that's 36 newtons for every meter per second so that's this many units of force per unit of speed and in the second case, we are taking this run here is v 2 minus v 1 this 2.5 being v 2 and 1.25 being v 1 and that's the denominator and the numerator is going to be F w 2 minus F w 1. So we are finding the slope of this segment here and if these numbers were close to the same, we would say yeah... the resistance force increases linearly with velocity but 14 is significantly different from 36 so we'll have to conclude: no, the change in water resistance is not linear with respect to speed because the slope of this resistance vs. velocity graph changes with velocity.

