Question
(a) What is the average power consumption in watts of an appliance that uses of energy per day? (b) How many joules of energy does this appliance consume in a year?
Final Answer
a)
b)
Solution video
OpenStax College Physics, Chapter 7, Problem 35 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
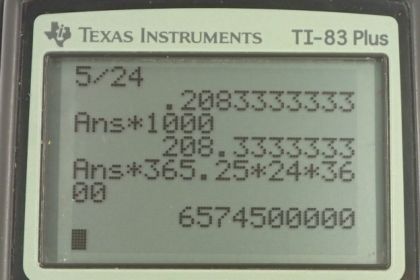
Video Transcript
This is College Physics Answers with Shaun Dychko. The power consumption of an appliance is the work done divided by the time. So the work we're told is five kilowatt hours of energy used. This isn't necessarily the useful work done by the way. This could also be thought of as the energy consumed and they seem to use E and W interchangeably in the textbook. So, we understand that this is the energy. So the energy is five kilowatt hours and that energy is used up in a day so we have to convert the time units into hours in order for the hours to cancel. We could have converted the numerator into joules and then the denominator into seconds if we had wanted to but I find that this is a bit easier. So we have one day times 24 hours per day and so we have five divided by 24 gives us the answer in kilowatts which we then convert into watts because the question tells us to give our answer in watts. So we have 0.2083 kilowatts multiplied by 1000 watts per kilowatt. Then we have 208 watts of power. Then how many joules of energy does it consume in a year? Well we're going to solve this for w by multiplying both sides by t and we end up with the energy consumed is going to be the power consumed multiplied by the time. So that's 208.33 joules per second where I've written watts in these units of joules per second instead, so that it's just easier to see how when you multiply by the time expressed in seconds we end up with joules. So that's one year multiplied by 365 and a quarter days per year times 24 hours per day times 3600 seconds per hour and this gives us 6.57 times ten to the nine joules of energy consumed in a year.