Question
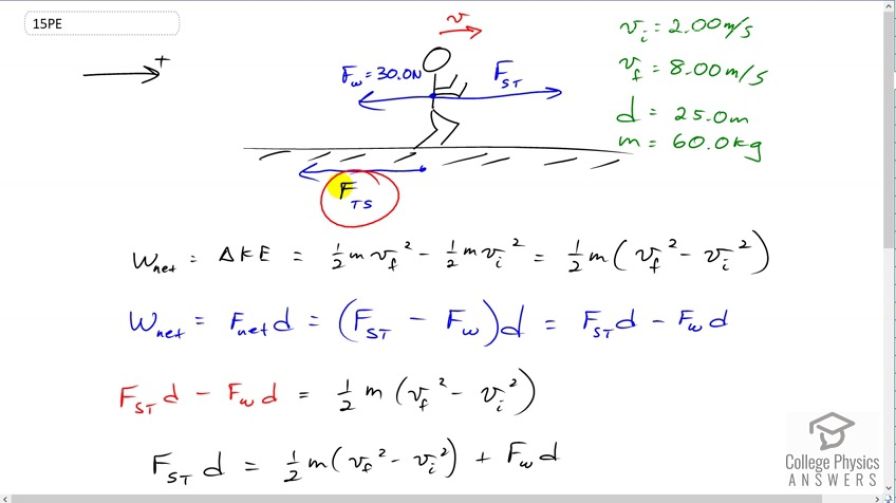
Using energy considerations, calculate the average force a 60.0-kg sprinter exerts backward on the track to accelerate from 2.00 to 8.00 m/s in a distance of 25.0 m, if he encounters a headwind that exerts an average force of 30.0 N against him.
Final Answer
Solution video
OpenStax College Physics, Chapter 7, Problem 15 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Given some information about this sprinter, we're supposed to find the force that the sprinter exerts on the track. So that's F subscript ts for the force on the track due to the sprinter. This is going to be equal in magnitude but opposite in direction to the force exerted on the sprinter due to the track. These are Newton's Third Law pairs, these two forces. So we can find this force, the force on the sprinter due to the track based on energy considerations. Now let's begin though by writing down the data. We have the initial speed of the sprinter is two meters per second and the final speed is eight. They achieved this change in speed over a distance of 25 meters and the mass of the sprinter is 60 kilograms. So we know that the net work done on the sprinter equals their change in kinetic energy. That's the work energy theorem and the change in kinetic energy is one half m v f squared minus one half m v initial squared. We can factor out the one half m to write it more concisely like that. One half m times v f squared minus v i squared. We also know that the net work is the net force on the sprinter multiplied by the displacement over which that force is applied. The net force is going to be the force on the sprinter due to the track to the right and that's positive. Then we have the force due to the wind going backwards so I wrote a minus sign there because it's in the negative direction and that gets multiplied by the displacement. Then we'll distribute the d into the brackets there, Fst d minus F w d. Okay. Then this can be used to replace the net work term in this expression and so we have the force on the sprinter due to the track times displacement, minus the force due to the wind, times displacement, equals the one half m v f squared minus v i squared. We want to solve for Fst here. So we'll add Fw d to both sides and then we get this line. Then we'll divide both sides here by d and then we have an expression for the force on the sprinter due to the track. So it's one half m times vf squared minus vi squared, plus F, force of the wind times displacement, all divided by displacement. So it's one half times 60 times eight meters per second squared, minus two meters per second squared, plus 30 newtons times 25 meters, all divided by 25 meters which gives 102 newtons. Now the force on the track due to the sprinter is what we want to find and that's going to be the negative of the force on the sprinter due to the track. So our answer is negative 102 newtons.
