Question
Integrated Concepts: (a) What force must be supplied by an elevator cable to produce an acceleration of against a 200-N frictional force, if the mass of the loaded elevator is 1500 kg? (b) How much work is done by the cable in lifting the elevator 20.0 m? (c) What is the final speed of the elevator if it starts from rest? (d) How much work went into thermal energy?
Final Answer
Solution video
OpenStax College Physics, Chapter 7, Problem 64 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
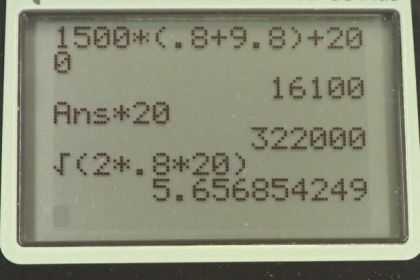
This is College Physics Answers with Shaun Dychko. We have an elevator that has an acceleration of .800 meters per second squared. And we'll assume that this is upwards, because upwards is usually the positive direction. And there's a friction force of 200 newtons which is gonna be downwards. And the mass of this elevator and occupants combined is 1500 kilograms. The free body diagram the elevator consist of the tension force in the cable upwards, and then the friction force and gravity both downwards. So in part A, we're going to figure out what force must be applied by this cable. So what is this tension force? So the tension force upwards, minus the gravity downwards, minus the friction force downwards is the net vertical force; and that's gonna be mass times vertical acceleration. And, so we can add force of gravity and force of friction to both sides. And a little note about minus signs, you might see other teachers legitimately write a plus sign here and a plus sign there. And I think if you're being very rigorous, it would be more correct is put pluses here, but I prefer not to. Because I like to remind myself of the direction of the forces using pluses and minuses in this formula. And then the terms will all just be magnitudes. So I’m gonna put positive m g in place of f g which would make it, you know, minus m g in the end. And put positive 200 in place of this force of friction, which would be minus 200 in the end. So after doing all this we end up with tension force is; mass times acceleration plus force of gravity plus friction. So that’s m a plus m g plus force of friction. And then we can factor out the common factor m here. And we have m times a plus g plus the force of friction and then we plug-in numbers; so we have 1500 kilograms times .8 meters per second squared, plus 9.8 meters per second squared, plus 200 newtons friction, giving us 16100 newtons is the tension force. Part B asked us how much work is done by this force in the cable? So that is the tension force multiplied by the displacement that's parallel to the tension force, but there's, no big deal there because they're both going in the same direction. And it’s the elevators going 20 meters upwards positive, and so is the tension force also is going upwards. And the product of these is 3.22 times ten to the five joules. That’s the work done by the force in the cable. Part C asks, what’s the final speed of the elevator if it starts at rest? So v initial is zero, now we know that the net work done on the elevator is going to be its change in kinetic energy. So that’s one half m times v final squared minus one half m v initial squared. The initial speed we’re told is zero. And so that makes the net work one half m v final squared. And, so this v final is what we’re trying to find. The net work done also can be thought of as the net force multiplied by the displacement. And that's going to be m a times d. And so we'll substitute this in place of net work, and we do that here. So we have m a d equals one half m v f squared. So we’ll divide both sides by m and multiply both sides by two. And then switch the sides around, and then take the square root of both sides. And we get v f equals square root two a d. So that’s the square root of two times .8 meters per second squared acceleration, times 20 meters displacement, and we get 5.66 meters per second. Then the question in part D is, what’s the work done by the friction force? Oh, and I should have a negative here. So, the friction force is downwards and the displacement is upwards. And so technically you should have a cosine of the angle between the displacement and the friction. In this case that would be 180 degrees which is negative one in other words. So put a negative one there and we have the work done by the friction is 200 newtons times 20 meters times negative one, which is negative 4.00 times ten to the three joules. I should add that part D of this question asks how much work went into thermal energy? And the answer to that is the whatever the work done by friction is what’s turned into thermal energy. I guess the answer for the thermal energy is going to be the positive of this. So, you might say that positive 4.00 times ten to the three joules is the amount of work that went into the thermal energy.