Question
Very large forces are produced in joints when a person jumps from some height to the ground. (a) Calculate the magnitude of the force produced if an 80.0-kg person jumps from a 0.600–m-high ledge and lands stiffly, compressing joint material 1.50 cm as a result. (Be certain to include the weight of the person.) (b) In practice the knees bend almost involuntarily to help extend the distance over which you stop. Calculate the magnitude of the force produced if the stopping distance is 0.300 m. (c) Compare both forces with the weight of the person.
Final Answer
Solution video
OpenStax College Physics, Chapter 7, Problem 52 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
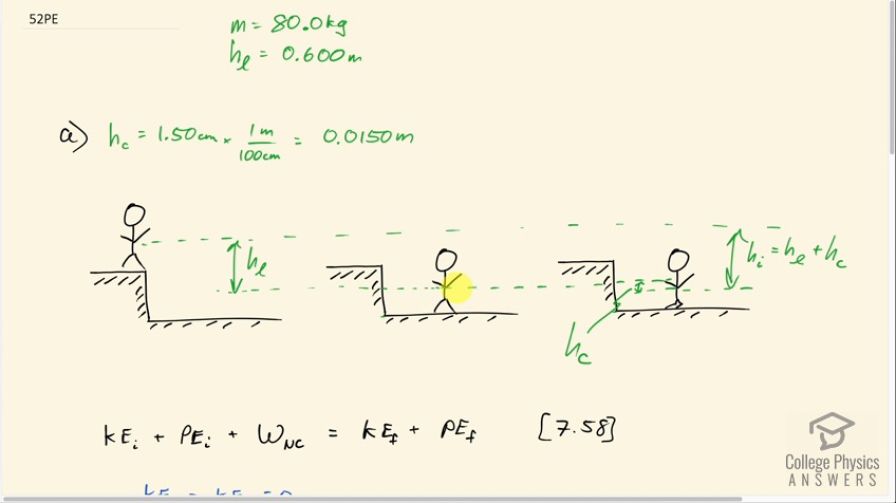
This is College Physics Answers with Shaun Dychko. A person jumps from a ledge which is 0.6 meters above the ground and then they land and then their joints will compress some distance so I have labeled that the height of compression with a letter 'c' for compression and the h l labels this height of the ledge. I could have written h l from the ground here to the ledge— that will be the same— but instead I made a dotted line from the person's center of mass at the beginning to their center of mass when they initially touch the ground before any compression happens and then this level is also being compared with their final height after compression happens and it's this final height that we want to compare to the very initial height. And so this h i—the initial height then— up here compared to where they will end up at the end we'll call this the zero level this is the y equals 0 position. That initial height then is going to be the height of the ledge from their center of mass when they just begin touching and their center of mass at the top of the ledge h l plus this height of compression as well. So this is the total height traveled is this height of the ledge plus the height compressed. Okay! So this is h i is what we are going to use in our initial potential energy formula. Now from equation [7.58] we know that the initial kinetic plus the initial potential energies plus the work done by a non-conservative force and this would be the work done by the joints— it's gonna be F J times the amount of compression— equals the final kinetic energy plus the final potential energy. This is equation [7.58] and it's a way of stating conservation of mechanical energy. So the initial and final kinetic energies are both zero because they start at rest and they end at rest here after compression and the final potential energy is zero because we are defining this to be our zero level where they end up after compression. So that means there's only this term and this term and this can be brought to the right hand side by subtracting it from both sides and we end up with the work done by the non-conservative force is the negative of the initial potential energy so that's negative mg times h i. So the work done by the non-conservative force is the force exerted by the joints that we want to find multiplied by the distance over which that force is acting which is this compression distance h c. And so we say F Jh c equals negative mgh substituting this in place of work, W NC. And then we divide both sides by the amount of compression and we have a formula for the force exerted by the joint. So it's gonna be negative mg initial height at the top of the ledge divided by the amount of compression. So that's negative 9.8 newtons per kilogram times 80.0 kilograms times 0.600 meters plus 0.0150 meters— this is the amount of compression in part (a)— and then we are dividing by negative 0.0150 meters and this negative comes from the fact that this displacement is downwards whereas this h i is the displacement upwards compared to here. Okay! So we end up with 3.21 times 10 to the 4 newtons. And then in part (b), the formula is the same but the amount of compression is different so we have 0.300 meters of compression so we have 0.600 meters—initial height of the ledge— plus the 0.300 meters compressed divided by negative 0.300 meters and multiplying by the weight and we get 2.35 times 10 to the 3 newtons which is an order of magnitude less than the force on the joints in part (a) and so now we compare these two forces to the weight. So we have 32144 newtons in part (a) divided by 80.0 kilograms times 9.8 newtons per kilogram which is 41.0. So the force on the joints is greater than the weight by a factor of 41 times. And then in part (b) with 0.300 meters of compression due to leg bending, there's a force of only 2352 newtons divided by the weight which is greater by a factor of 3.00 and this can be easily tolerated by the joints whereas this would probably lead to some damage of some kind.

