Question
A toy gun uses a spring with a force constant of 300 N/m to propel a 10.0-g steel ball. If the spring is compressed 7.00 cm and friction is negligible: (a) How much force is needed to compress the spring? (b) To what maximum height can the ball be shot? (c) At what angles above the horizontal may a child aim to hit a target 3.00 m away at the same height as the gun? (d) What is the gun’s maximum range on level ground?
Final Answer
a)
b)
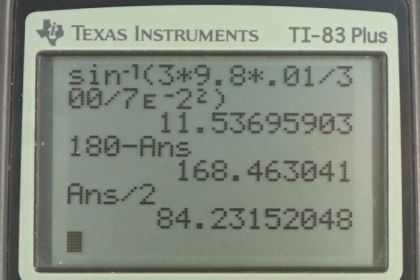
c) or
d)
Solution video
OpenStax College Physics, Chapter 7, Problem 63 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This toy gun has a spring constant of 300 newtons per meter and the mass of the steel ball inside of it is 0.01 kilograms, I've to convert the ten grams to kilograms, and the spring inside of it gets compressed seven centimeters which is seven times ten to the minus two meters. So part A asks for the force that the spring applies on the pellet. So that's going to be negative 300 newtons per meter times the seven centimeters and this works out to negative 21 newtons. The negative sign just means the force is in the opposite direction to the compression of the spring. In part B, we're asked to figure out what maximum height the ball could be shot if it was shot straight up. So the elastic potential energy in the spring when it's compressed is going to get converted entirely into gravitational potential energy because at the very top of its height it will have no kinetic energy at that point and all of this energy which is initially elastic potential energy will have turned entirely into gravitational potential energy. So we divide both sides by mg to solve for h and we get the height is the spring constant times the amount the spring is compressed squared, divided by two times the mass of the steel ball times gravitational field strength. So that's 300 newtons per meter times seven centimeters squared, divided by two times 0.01 kilograms times 9.8 newtons per kilogram giving a maximum possible height of 7.5 meters. In part C, we're asked to find what angles above the horizontal a child could aim the gun to hit a target three meters away. The target is at the same height as the gun which is a nice piece of information because that means we can use the range formula in that case. So the gun is going to shoot the steel ball at some angle theta we're going to find, such that it goes here which is three meters away from where it started. So the range is three meters. Now, we're going to find two angles such that this is possible. One angle is going to be really shallow and the other angle is going to be really steep and it'll reach the same horizontal position. So the range formula from chapter three is the initial speed squared times sine of two times this angle theta, all divided by g. We're going to solve for theta so multiply both sides by g over v naught squared, and then switch the sides around. We have sine two theta is range times gravitational field strength divided by v naught squared. Then we'll take the inverse sine of both sides and we get two theta on the left equals the inverse sine of r g over v naught squared and then divide both sides by two. We get this formula for the angle, inverse sine of range times acceleration due to gravity divided by initial speed squared, all divided by two. Now we can't directly use this formula yet because we don't know what the initial speed is. But we can find it because when this gun which is shaped like this I suppose, it has a spring inside of it, and its spring is compressed and when it's compressed it will have some elastic potential energy and all of that elastic potential energy will get turned into kinetic energy when the pellet exits the gun. So we can find the initial speed of the pellet at this point by saying the elastic potential energy equals kinetic energy when the pellet comes out of the gun. So we multiply both sides by two and divide both sides by m and we get v naught squared is k x squared over m. We'll substitute that in for v naught in this formula for theta. Now instead of dividing by v naught squared, I'm going to multiply by its reciprocal in order to avoid dividing fraction by a fraction. So we have theta is the inverse sine of range times g times m over k x squared, all over two. So theta is the inverse sine of three meters, times 9.8 meters per second squared, times 0.01 kilograms divided by 300 newtons per meter times seven times ten to the minus two meters, and that get's squared, all that is divided by two. Now, we're going to get two answers. The inverse sine of that whole numerator there is 11.537 but that is a reference angle and so if you consider the unit circle here, and perhaps you remember the acronym CAST which tells you which quadrants the trigonometric functions are positive in, we find that we have one solution here, this is our 11.537 degrees solution in the quadrant one, and quadrant two has all of the trigonometric functions positive and so we also have a solution here where this portion here, this angle between the terminal arm of the angle and the x axis is the reference angle. This is 11.537 degrees and the angle in standard position starting from the positive x axis is going to be -- we'll call this theta subscript two say, it's the second solution -- it's going to be the straight line angle of 180 degrees minus this reference angle of 11.537. So that gives us this 168.46 degrees. Then we have to divide both of those by two and we get 5.77 degrees and 84.2 degrees are the angles that the gun could be shot such that the pellet lands three meters from where it started. Then lastly, we're asked to find out what is the maximum possible range for this toy gun and that'll be v naught squared over g where an angle is chosen in this formula such that sine two theta is its maximum which is one. That occurs when theta is 45. So, we have v naught squared already, we have a formula for that over here, it's k x squared over m and so we substitute that in place of v naught squared. So k x squared over m times one over g, that gives 300 newtons per meter times seven times ten to the minus two meters squared, divided by 0.01 kilograms of mass times 9.8 meters per second squared, giving a maximum possible range of 15.0 meters.