Question
(a) How long will it take an 850-kg car with a useful power output of 40.0 hp (1 hp = 746 W) to reach a speed of 15.0 m/ s, neglecting friction? (b) How long will this acceleration take if the car also climbs a 3.00-m-high hill in the process?
Final Answer
Solution video
OpenStax College Physics, Chapter 7, Problem 38 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
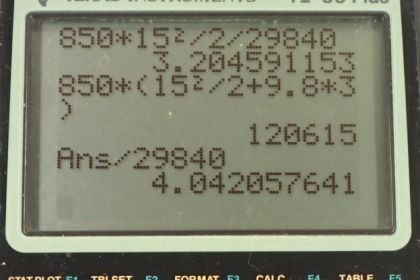
This is College Physics Answers with Shaun Dychko. An 850-kilogram car with 40 horsepower is going to begin at rest and then achieve a final speed of 15.0 meters per second and the question is how long will it take to accelerate from 0 to 15? We take this opportunity when we are writing down the stuff that we know to do any unit conversion so that we don't have to think about that during our work. So this 40 horsepower is 29840 watts when you multiply by 746 watts per horsepower. Okay! So power is work done divided by time and we are concerned with the car here so it's the power of the car equals the work done by the car divided by time and we are going to rearrange this for t later on but first, what work does the car do? Well, it's going to equal the net work because the force on the car, you know, it's the force that the car applies on the ground which the ground then in turn applies onto the car but that's, you know, a detail we don't need to concern with. What is important that there's only one horizontal force on the car and the car's responsible for it. And that means this is the net force which is parallel to the displacement and so it's the only force that is going to do any work because the only forces that do work are ones that have components parallel to displacement. So that means the force that the car is applying is the net force and therefore the work it does is the net work and that's important because we have a formula for net work from this work-energy theorem which says that the net work done equals the change in kinetic energy of the car. And so that is one-half mass times the final speed squared minus one-half mass times initial speed squared. So we can substitute this in place of work done by the car the initial speed being zero so this term is zero and so we have one-half mv f squared over t equals P. Then we multiply both sides by t over P and we get the time. So the time is mass times final speed squared over 2 times power. So that's 850 kilograms times 15.0 meters per second squared divided by 2 times 29840 watts which is 3.2 seconds. Now in part (b), the change in speed is the same so the change in kinetic energy, in other words, is the same but now the car's going to go up a hill which is 3 meters high. So we could use this formula but it gets complicated because now we have a gravity which has some component which is parallel to displacement now and you know then we have to assume that the hill is a perfectly flat slope and then figure out the what the component of gravity is parallel to the displacement and we don't wanna do any of that. That's why energy is nice because it's a scalar quantity meaning we don't need to concern ourselves with vectors and that makes our calculations more simple. So what we do know is the work done by the car is the work done by the non-conservative forces; it's the only other force here, there's no friction and it's a non-conservative force because it's adding energy to the system. Any force that adds mechanical energy or removes mechanical energy is a non-conservative force— that's the way I like to think about it. A more strict definition is to say that a non-conservative force, you know, it's path dependent the amount of energy that it adds or removes and that being true, it's more useful I think to think of it this way that non-conservative forces add or remove mechanical energy from the system. Okay! So this car for certainly is adding mechanical energy to the system because it's increasing the car's kinetic energy and it's also going to increase its potential energy. So this is equation [7.57] and so the change in kinetic energy is one-half mv f squared— I didn't bother writing the minus one-half mv i squared since it starts from rest— and then change in potential energy is the force of gravity multiplied by the change in height so mgh. So we can factor out the m and we have v f squared over 2 plus gh and that is 850 kilograms times 15.0 meters per second squared over 2 plus 9.80 times 3.00 meters and we get 120615 joules. Now that's what we are going to put in for the work done by the car in part (b) here and rearranging it for t as we did before and we get the time is the work done by the car divided by power. So that's 120615 joules divided by 29840 watts which is 4.0 seconds.